Consider a wire carrying a steady current, I placed in a uniform magnetic field →B perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do not work. This implies that
Maximum possible magnetic field is B0+μ0I2πR
Minimum magnetic field at some point is zero if R<μ0I2πB0
Minimum magnetic field at some point is B0−μ0I2πR, if R>μ0I2πB0
Magnetic field at a point on its axis is B0.
The correct Answer is:a, b, c, d
Magnetic field lines due to the current in cylinder are circles perpendicular to the length of cylinder and hence at some points, its magnetic field will become parallel or anti-parallel to the applied magnetic field.
Maximum possible magnetic field is obtained for points where the field due to cylinder is maximum (points on its surface) and parallel to the applied magnetic field. Hence B0+μ0I2πR will be the maximum possible magnetic field at some suitable point on its surface.
Option (a) is correct.
We know that at some point on its surface, the applied magnetic field is anti-parallel to the field created by current. But in case of the minimum possible magnetic field, there is a little twist.
Let us suppose that the applied magnetic field is less than the maximum field due to current, then there will be a point on either side of the surface where the field due to current is equal to the applied field and thus the resultant becomes zero for these points.
B0<μ0I2πR⇒R<μ0I2πB0
Hence option (b) is correct.
If applied field is more than the maximum possible field due to current, then the minimum magnitude of magnetic field will be certainly on the surface and its magnitude will be B0−μ0I2πR . This is the case
when B0>μ0I2πR⇒R>μ0I2πB0
Option (c ) is correct.
Option (d) is also correct because magnetic field due to the current is zero at a point on the axis of the cylinder.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (ASSERTION TYPE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
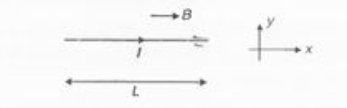
the force on current carrying wire placed in uniform magnetic field B as shown in figure is
View SolutionA 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
View Solution
Knowledge Check
A wire carrying a current i is placed in a uniform magnetic field in the form of the curve y=asin(πxL)0≤x≤2L. The force acting on the wire is
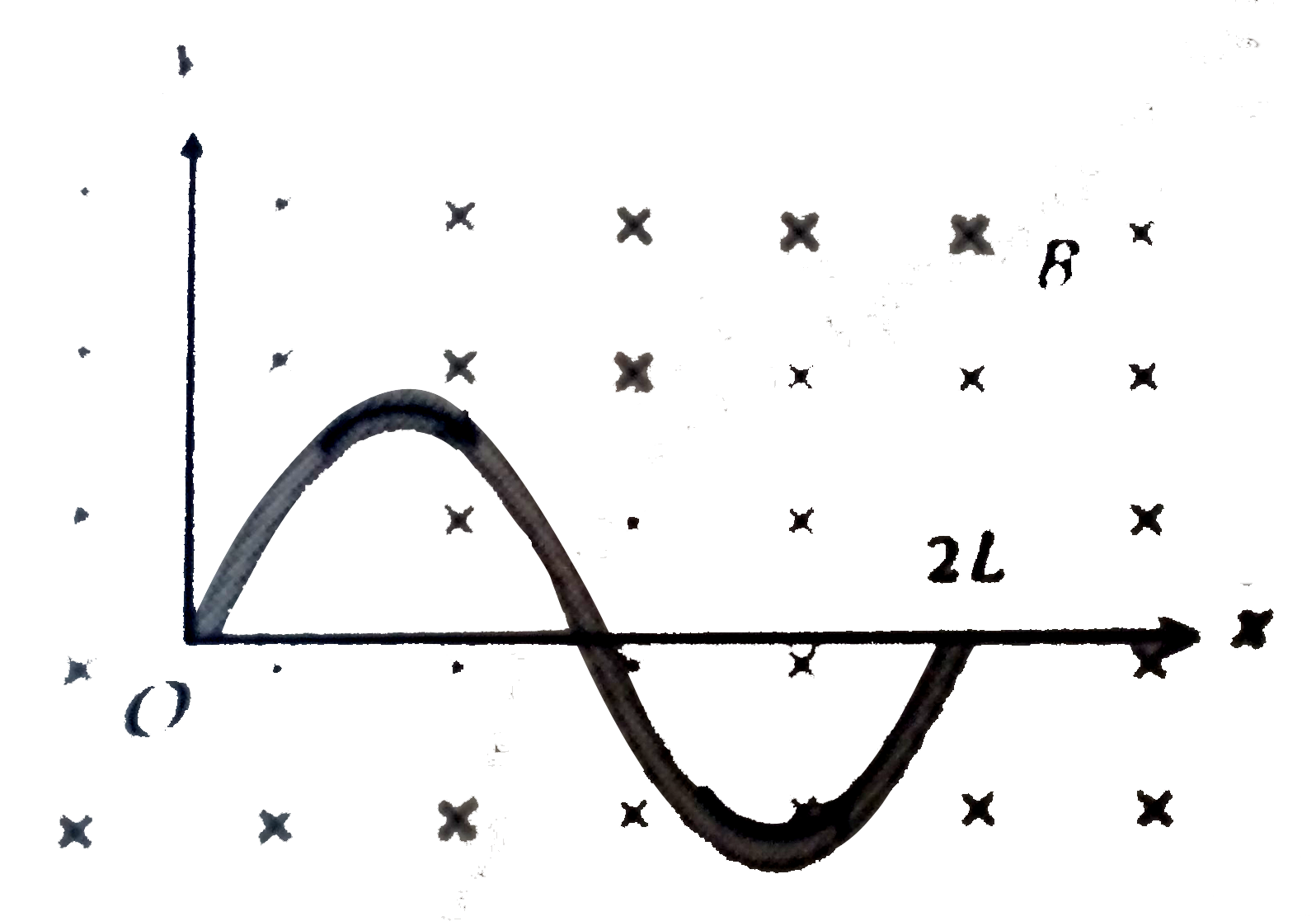 AiBLπBiBLπC2iBLDzero
AiBLπBiBLπC2iBLDzeroAn 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44NA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
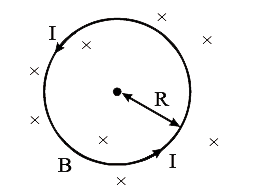 ABIRB2πBIRCπBIRD2BIR
ABIRB2πBIRCπBIRD2BIR
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
View SolutionA current-carrying conductor placed in a uniform magnetic field experiences maximum force when the conductor is placed parallel to the magnetic field.
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionA straight wire of length 1 m, and carrying a current of 1.8 A, is placed in a uniform magnetic field of induction 2T. If the magntic field is perpendicular to the length of the wire, then the force acting on the wire is
View Solution
