In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.
zero at a point on axis of inner cable
zero at a point outside the cable
maximum at the surface of inner cable
zero in between inner and outer cable
The correct Answer is:a, b, c
If we apply Ampere.s law, then the magnetic field inside the inner cable is same as that due to a cylindrical wire. Hence, the field will be zero at a point on the axis of cable and it becomes maximum at the surface of theinner cable. Outside the inner cable, the field starts decreasing and when the outer cable is also being included in the amperes loop then the magnetic field further goes down due to decrease in enclosed current because the outer cable carries current in the opposite direction. Finally for points outside the co-axial cable, the net current enclosed in amperes loop becomes zero (equal and opposite currents) and hence the magnetic field becomes zero for all points outside the cable. There is a magnetic field in the gap between the inner and outer cables. Hence options (a), (b) and (c) are correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (ASSERTION TYPE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) r>a, (b) a<r<b and (c) b>r>c

View SolutionThere is one long coaxial cable which consists of two concentric cylinders of radii a and b. Central conductor carries steady current I and outer conductor acts as return path for the current. (i) Calculate energy stored in the magnetic field of length l of such a cable. (ii) Calculate self-inductance for l length of this cable.
View Solution
Knowledge Check
In a coaxial, straght cable, the central conductor and the outer conductor carry equal currents in opposite directions.The magnetic field is non-zero.
 Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductors
Aoutside the cableBinside the inner conductor except axis of the conductorCall the point inside the outer conductor and outside inner conductorDonly on axis of conductors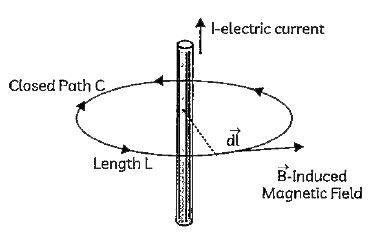
If two conductors carry current in opposite direction, then:Athere is no force between themBforce is repulsiveCforce is attractiveDindependent of forceA coaxial cable consists of a thin inner conductor fixed along the axis of a hollow outer conductor. The two conductor carry equal currents in opposite directions. Let B1andB2 be the magnetic fields in the region between the conductors and outside the conductor, respectively. Then,
AB1≠0,B2≠0BB1=B2=0CB1≠0,B2=0DB1=0,B2≠0
Two long straight conductors are held parallel to each other 7cm apart. The conductors carry currents of 9A and 16A in opposite directions. The distance of neutral point from the conductor carrying 16A current is
View SolutionThe two linear parallel conductors carrying currents in the opposite direction…………………each other.
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionThe direction of force on a current carrying conductor in a magnetic field is given by
View SolutionMagnetic lines of force due to a straight conductor carrying current are
View Solution
