There is one circular loop of a uniform wire whose radius is R. Electric current I enters at one point on its circumference and leaves at a diametrically opposite point. What will be the net magnetic field intensity at the centre of the loop?
μ0i4r
μ0i2r
μ0ir
Zero
The correct Answer is:d
To find the net magnetic field intensity at the center of a circular loop of uniform wire with radius R, where electric current I enters at one point on its circumference and leaves at a diametrically opposite point, we can follow these steps:
Step 1: Understand the Current Distribution
The current I enters the loop at point A and exits at point B, which is diametrically opposite to A. Since the current is uniformly distributed along the wire, the current flowing through each half of the loop will be I/2.
Step 2: Analyze the Magnetic Field Contribution from Each Half
The circular loop can be divided into two halves:
- The upper half (from A to B)
- The lower half (from B to A)
Using the Biot-Savart law, we can determine the magnetic field at the center of the loop due to each half.
Step 3: Calculate the Magnetic Field from the Upper Half
For the upper half of the loop, the magnetic field at the center (let's call it B1) can be calculated using the formula:
B1=μ0(I/2)4πR⋅θ
where θ is the angle subtended by the semicircular wire at the center, which is π radians for a semicircle. Thus,
B1=μ0(I/2)4πR⋅π=μ0I8R
The direction of this magnetic field (using the right-hand rule) will be into the plane of the loop.
Step 4: Calculate the Magnetic Field from the Lower Half
For the lower half of the loop, the magnetic field at the center (let's call it B2) is similarly calculated:
B2=μ0(I/2)4πR⋅θ=μ0I8R
However, the direction of this magnetic field will be out of the plane of the loop.
Step 5: Determine the Net Magnetic Field
Now, we have:
- B1 (from the upper half) directed into the plane
- B2 (from the lower half) directed out of the plane
Since both magnetic fields have the same magnitude but opposite directions, they will cancel each other out:
Bnet=B1−B2=μ0I8R−μ0I8R=0
Conclusion
The net magnetic field intensity at the center of the loop is zero.
The current I enters the loop at point A and exits at point B, which is diametrically opposite to A. Since the current is uniformly distributed along the wire, the current flowing through each half of the loop will be I/2.
The circular loop can be divided into two halves:
- The upper half (from A to B)
- The lower half (from B to A)
For the upper half of the loop, the magnetic field at the center (let's call it B1) can be calculated using the formula:
B1=μ0(I/2)4πR⋅θ
where θ is the angle subtended by the semicircular wire at the center, which is π radians for a semicircle. Thus,
B1=μ0(I/2)4πR⋅π=μ0I8R
The direction of this magnetic field (using the right-hand rule) will be into the plane of the loop.
For the lower half of the loop, the magnetic field at the center (let's call it B2) is similarly calculated:
B2=μ0(I/2)4πR⋅θ=μ0I8R
However, the direction of this magnetic field will be out of the plane of the loop.
Now, we have:
- B1 (from the upper half) directed into the plane
- B2 (from the lower half) directed out of the plane
Bnet=B1−B2=μ0I8R−μ0I8R=0
The net magnetic field intensity at the center of the loop is zero.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)
79 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Revision Exercises (Numerical Problems )
18 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A current I enters a uniform circular loop of radius R at point M and flows out at N as shown in the Fig. Obtain the net magnetic field at the centre O of the loop.
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View Solution
Knowledge Check
There is one circular loop of wire of radius R, carrying current I and magnetic field at its centre is B0, due to its own current. The loop is bent along its diameter at right angle. What will be the net magnetic field at the centre of the loop?
AB0√2BB0√2C2B0√2DB0√3What will be magnetic field at centre of current carrying circular loop of radius R?
Aμ0I4πRBμ0I2πRCμ0I2RDzeroABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
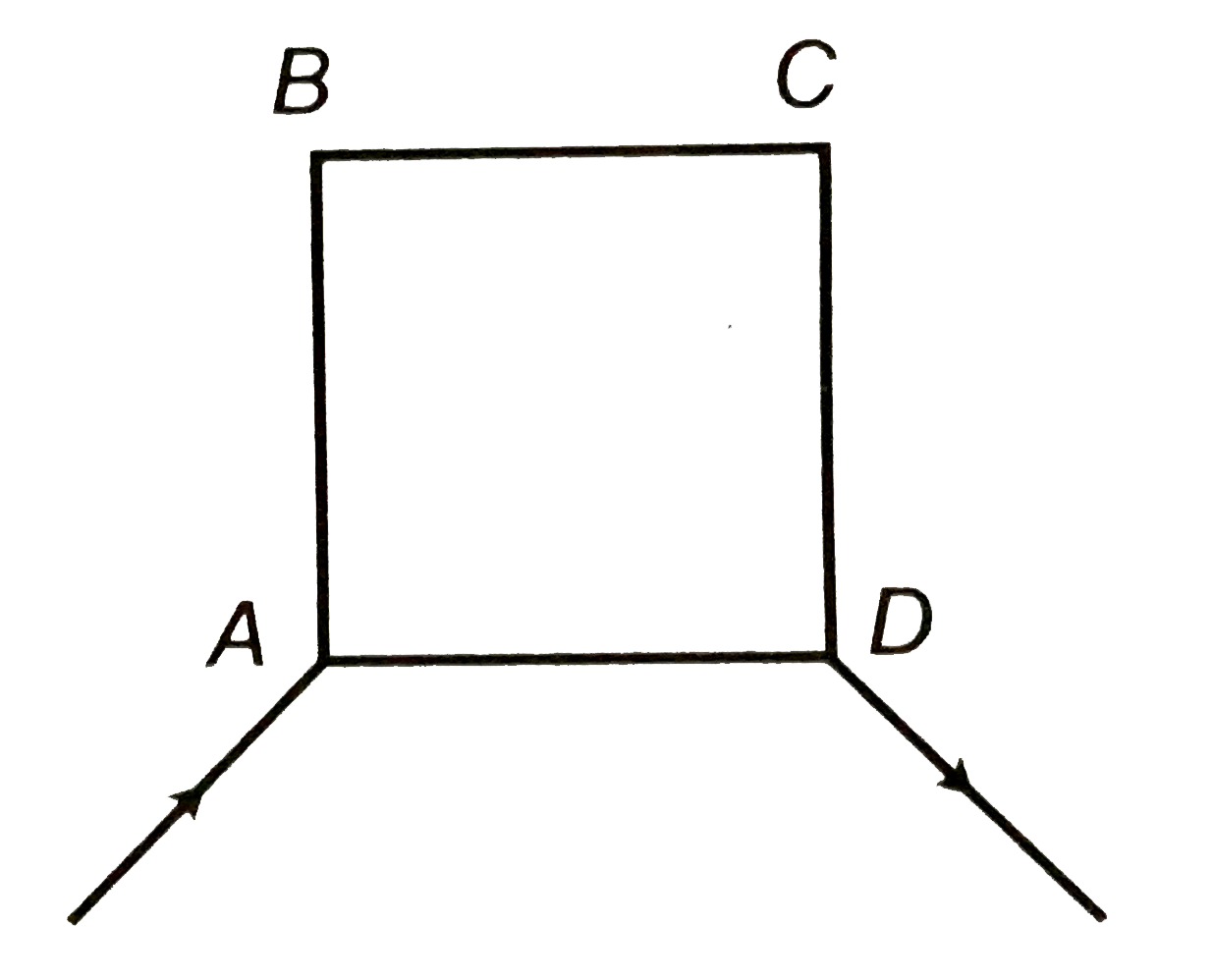 Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Equal current I flows in two segments of a circular loop in the direction shown in figure. Radius of loop is R. What is the magnitude of magnetic field induciton at the centre of the loop?
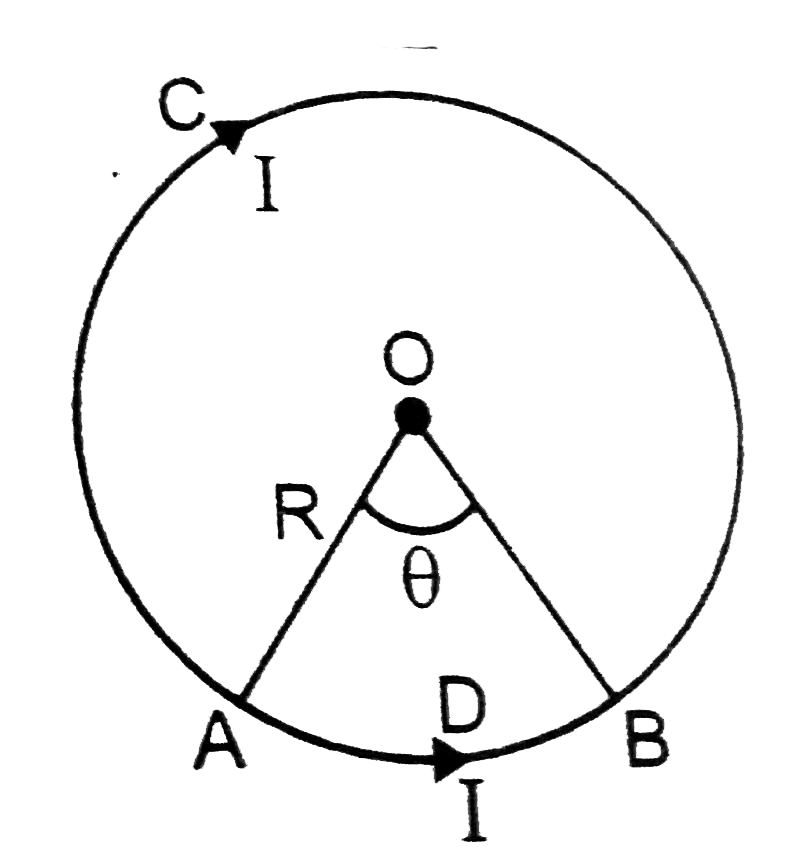
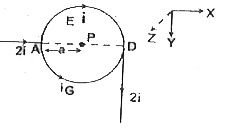
View SolutionIn the shown figure a current 2i is flowing in a straight conductor and entering along the diameter of the circular loop of similar conductor through the point A. The current is leaving the loop along another similar semi-infinite conductor parallel to the plane of the loop through the point D. what is the magnetic field at the centre of the loop P ?
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
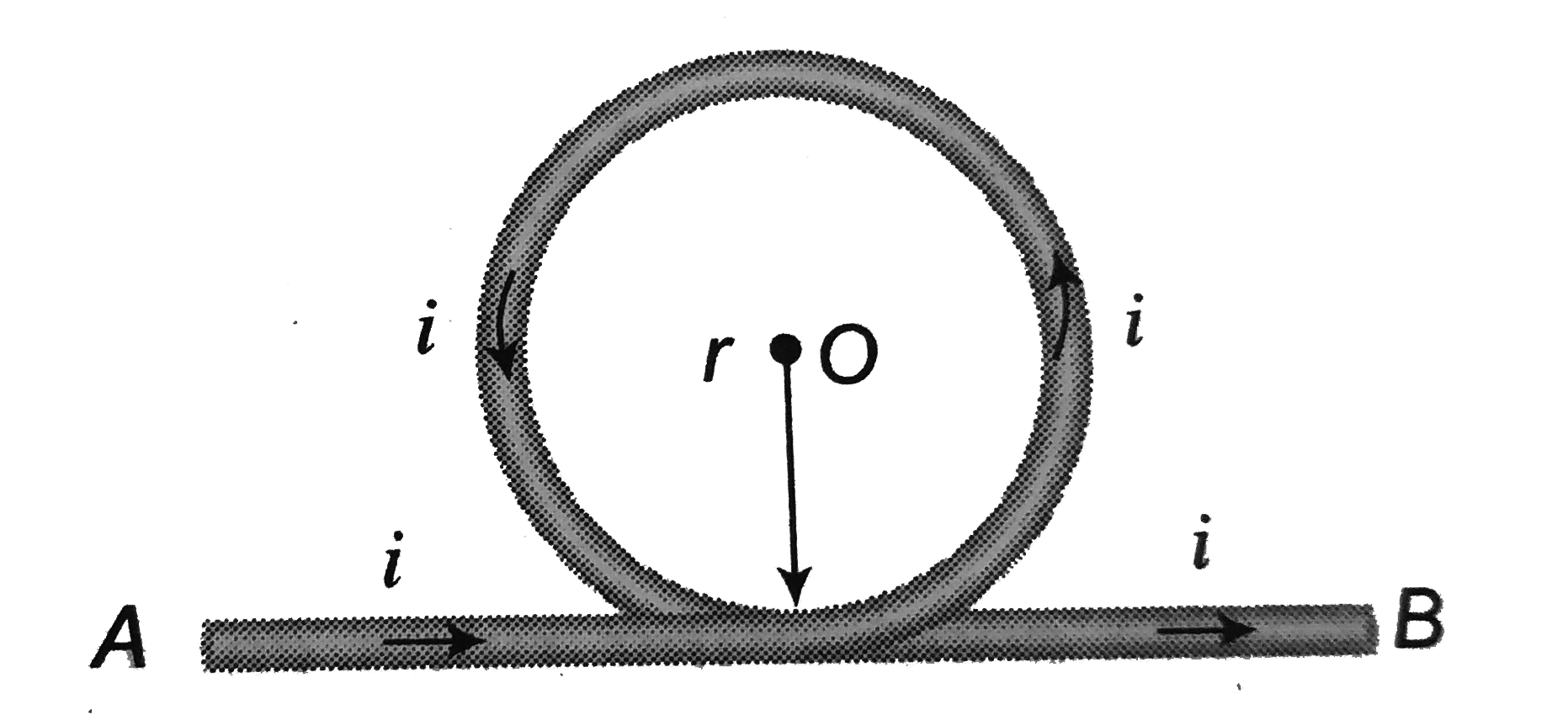
View Solution
