Consider a wire carrying a steady current, I placed in a uniform magnetic field perpendicular to its length. Consider the charges inside the wire. It is known that magnetic forces do not work. This implies that
the motion of charges inside the conductor is unaffected by B since they do not absorb energy.
some charges inside the wire move to the surface as a result of B.
if the wire moves under the influence of B, no work is done by the force.
if the wire moves under the influence of B, no work is done by the magnetic force on the ions that is assumed fixed within the wire.
The correct Answer is:b, d
Let us consider a wire connected to a battery between two rails and a uniform external magnetic field as shown in the figure.

Due to current flowing through the wire AB on application of external electric field (battery), the free charges inside the wire will start drifting towards the positive terminal of the battery with an average velocity v.
The force acting on the charge due to external magnetic field B will be:
The force acting on the free charges will be given by the left-hand rule and is from south to north (if the charge is positive) and from north to south (if the charge is negative).
Now, due to this force experienced by the moving charges, there will be shifting of the charges on the surface of wire and it will also contribute to the net force acting on the wire.
When the wire moves under the influence of this magnetic force, the ions fixed inside the wire are dragged along with it. So, the velocity of ions is now towards the north direction and due to magnetic field, they will experience a force along the length of wire (towards west).
Since, the displacement of ions and force acting on them are mutually perpendicular, the network done on the ions by the magnetic force will be zero.
Also, force acting on wire of length l and carrying a current I in an external field is given by:
Here , = angle between length of the wire and external magnetic field
Since the displacement of wire is along the direction of force acting on it, work will be done on the wire if it moves under the influence of .
Thus, options (b) and (d) are correct.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) (Very Short Answer Type Questions )
5 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) (Short Answer Type Questions )
6 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
6 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
the force on current carrying wire placed in uniform magnetic field B as shown in figure is
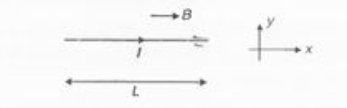
View SolutionA 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
View Solution
Knowledge Check
A wire carrying a current i is placed in a uniform magnetic field in the form of the curve y=asin(πxL)0≤x≤2L. The force acting on the wire is
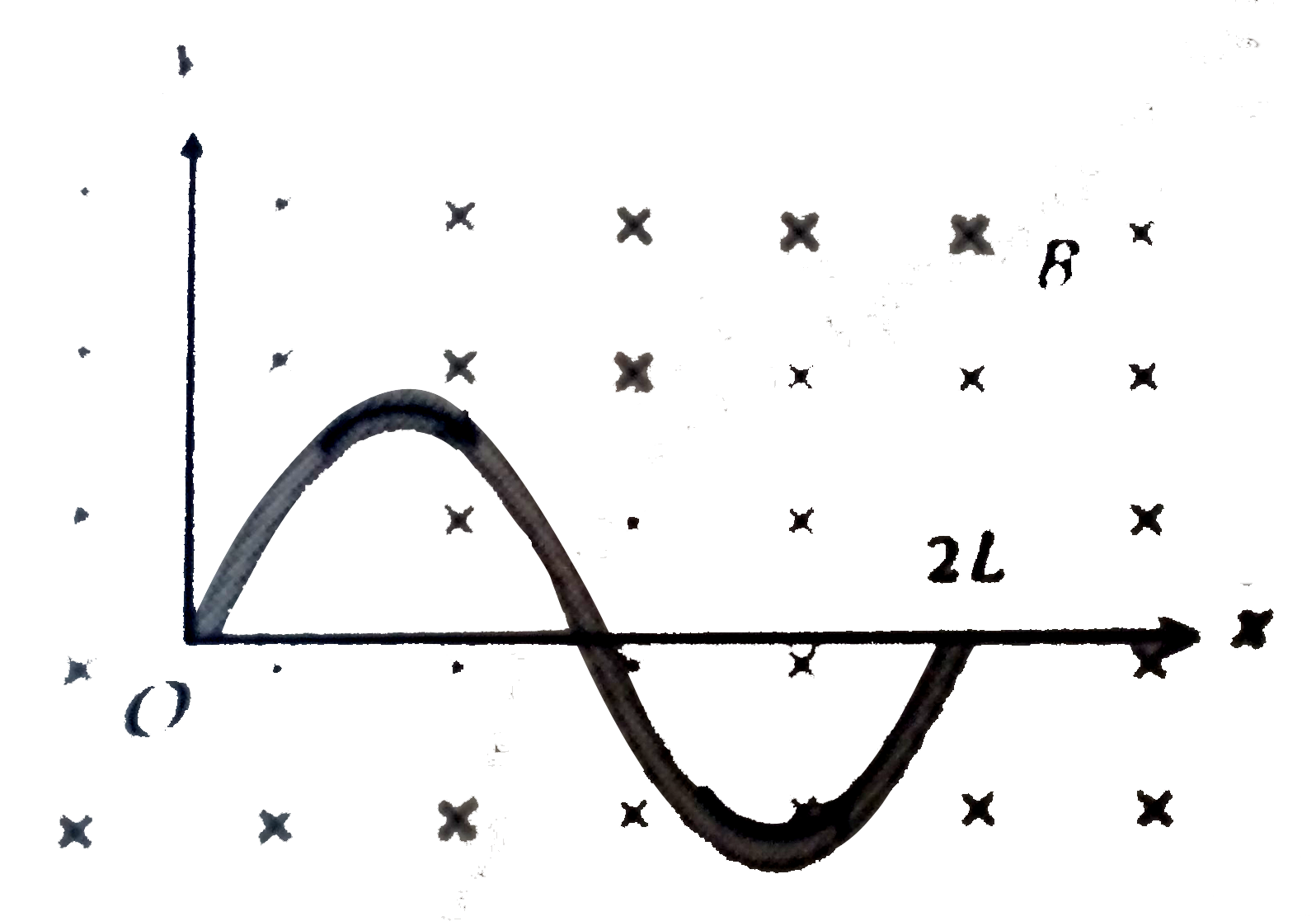 AiBLπBiBLπC2iBLDzero
AiBLπBiBLπC2iBLDzeroAn 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44NA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
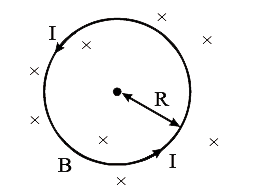 ABIRB2πBIRCπBIRD2BIR
ABIRB2πBIRCπBIRD2BIR
A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire ?
View SolutionA current-carrying conductor placed in a uniform magnetic field experiences maximum force when the conductor is placed parallel to the magnetic field.
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionAn electric wire of resistance R carries a current I. When a magnetic field is applied perpendicular to the wire, the
View SolutionA straight wire of length 1 m, and carrying a current of 1.8 A, is placed in a uniform magnetic field of induction 2T. If the magntic field is perpendicular to the length of the wire, then the force acting on the wire is
View Solution
