Question

The gyro-magnetic ratio of an electron in an H-atom, according to Bohr model, is

Options

A. independent of which orbit it is in.
B. negative.
C. positive .
D. increases with the quantum number n.

Answer

a, b

Explanation

An electron of charge e and mass m is revolving in n orbit of hydrogen atom. Then, according to Bohr.s theory, the angular momentum of the electron will be given by
`L = (nh)/(2 pi)` ….(i)
where h = Planck.s constant

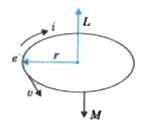
Let us consider that the electron is revolving in a circle of radius and with a velocity v. The time period of electron in the orbit will be :
`T = ("Circumference ")/("Velocity") = (2 pi r)/v`
The current i due to the motion of electron is the charge flowing through that time period is ` i = (- e)/T`
`rArr " " i = (-e)/((2 pi r)/v) = (- ev)/(2 pi r) `
The magnetic moment due to a current loop enclosing an area will be :
`M = iA = (- evA)/(2 pi r) = (- ev)/(2 pi r) xx pi r ^(2) " " [A = pi r^(2)]`
` rArr " " M = (-er v)/2 `.......(ii)
Multiplying and dividing (ii) with m, we get:
`M = (-e)/(2 m) mvr` ......(iii)
We know that, angular momentum of an object is given by :
`L = mvr` ....(iv)
Combining (iii) and (iv) , we get :
` M = (-e)/(2 m) L`
Gyromagnetic ratio of the electron ` = M/L`
` = (-e)/(2 m) ` = constant
It is negative constant value.
Therefore, options (a) and (b) correct.