Question

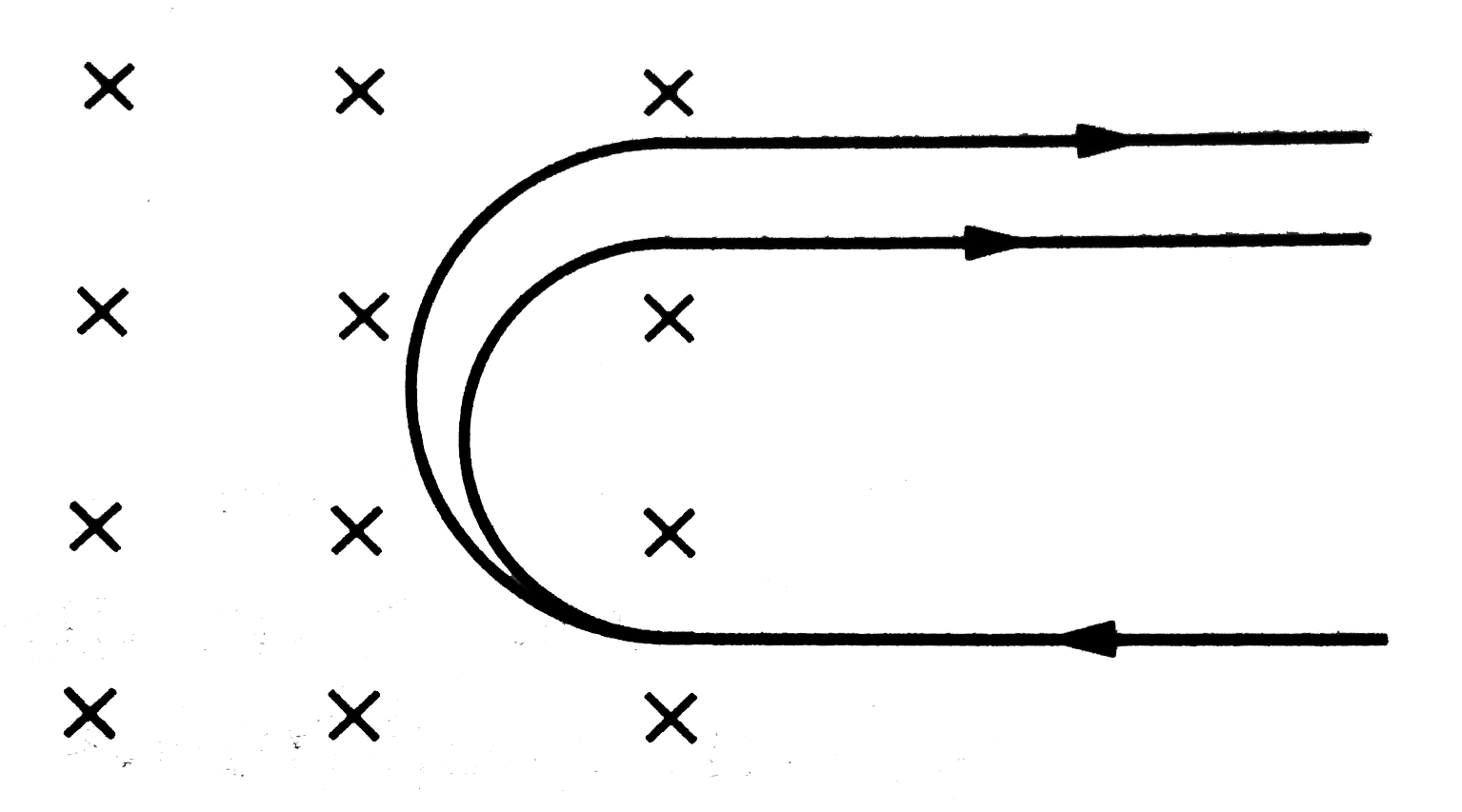
Two types of particles having same charge equal to $+2e$ but different masses are moving with a constant velocity of $6\times {10}^4$ m/s in the form of a beam. These particles suddenly encounter a perpendicular magnetic field in a rectangular region having intensity equal to $0.5$ T. It is found that particles emerge from the field in the backward direction from two different points. These points are at a distance 3 cm and $3.5$ cm from the incident beam. Find the ratio of their masses.

Explanation

To solve the problem of finding the ratio of the masses of two particles with the same charge moving in a magnetic field, we will follow these steps:

Step 1: Write down the given data
- Charge of the particles, \( q = +2e = 2 \times 1.6 \times 10^{-19} \, \text{C} \)
- Magnetic field intensity, \( B = 0.5 \, \text{T} \)
- Velocity of the particles, \( v = 6 \times 10^{4} \, \text{m/s} \)
- Distances from the incident beam where particles A and B emerge: \( d_A = 3 \, \text{cm} = 0.03 \, \text{m} \) and \( d_B = 3.5 \, \text{cm} = 0.035 \, \text{m} \)

Step 2: Calculate the radius of the circular paths
The radius \( r \) of the circular path followed by a charged particle in a magnetic field is given by the formula:
\( r = \frac{mv}{qB} \)
For particle A:
\( r_A = \frac{d_A}{2} = \frac{3 \, \text{cm}}{2} = 1.5 \, \text{cm} = 1.5 \times 10^{-2} \, \text{m} \)
For particle B:
\( r_B = \frac{d_B}{2} = \frac{3.5 \, \text{cm}}{2} = 1.75 \, \text{cm} = 1.75 \times 10^{-2} \, \text{m} \)

Step 3: Calculate the mass of particle A
Using the formula for the radius, we rearrange it to find the mass \( m \):
\( m_A = \frac{qBr_A}{v} \)
Substituting the values:
\( m_A = \frac{(2 \times 1.6 \times 10^{-19} \, \text{C})(0.5 \, \text{T})(1.5 \times 10^{-2} \, \text{m})}{6 \times 10^{4} \, \text{m/s}} \)
Calculating this gives:
\( m_A = \frac{(1.6 \times 10^{-19})(0.5)(1.5 \times 10^{-2})}{6 \times 10^{4}} = 0.4 \times 10^{-25} \, \text{kg} \)

Step 4: Calculate the mass of particle B
Similarly, for particle B:
\( m_B = \frac{qBr_B}{v} \)
Substituting the values:
\( m_B = \frac{(2 \times 1.6 \times 10^{-19} \, \text{C})(0.5 \, \text{T})(1.75 \times 10^{-2} \, \text{m})}{6 \times 10^{4} \, \text{m/s}} \)
Calculating this gives:
\( m_B = \frac{(1.6 \times 10^{-19})(0.5)(1.75 \times 10^{-2})}{6 \times 10^{4}} = 0.46 \times 10^{-25} \, \text{kg} \)

Step 5: Find the ratio of the masses
Now, we can find the ratio of the masses \( \frac{m_A}{m_B} \):
\( \frac{m_A}{m_B} = \frac{0.4 \times 10^{-25}}{0.46 \times 10^{-25}} = \frac{0.4}{0.46} \approx 0.87 \)

Final Answer
The ratio of the masses of the two particles is approximately:
\( \frac{m_A}{m_B} \approx 0.87 \)