A charged particle enters a magnetic field at right angles to the field. The field exists for a length equal to 1.5 times the radius of circular path of particle. The particle will be deviated from its path by
90∘
sin−1(2/3)
30∘
180∘
The correct Answer is:4
To solve the problem, we need to analyze the motion of a charged particle entering a magnetic field at right angles. Here's a step-by-step solution:
Step 1: Understand the scenario
A charged particle enters a magnetic field perpendicularly, which means it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path is denoted as r.
Hint: Remember that the force on a charged particle in a magnetic field is given by the Lorentz force, which causes circular motion when the particle enters at right angles.
Step 2: Determine the length of the magnetic field
According to the problem, the length of the magnetic field L is given as 1.5 times the radius of the circular path:
L=1.5×r
Hint: Identify the relationship between the length of the magnetic field and the radius of the circular path to understand how far the particle will travel in the field.
Step 3: Analyze the circular motion
When the particle enters the magnetic field, it will begin to move in a circular path with radius r. The time it takes for the particle to complete a full circle is determined by its speed and the radius.
Hint: Recall that the particle will continue in a circular path until it exits the magnetic field.
Step 4: Determine the angle of deviation
Since the length of the magnetic field L is 1.5r, the particle will not complete a full circular path. Instead, it will travel through the magnetic field and exit after covering a distance of 1.5r.
The particle will complete 1.5r2πr=1.52π of a full circle, which corresponds to an angle of:
θ=1.52π×360∘=540∘2π≈86.6∘
However, since the particle is entering at right angles and the field length is more than the radius, it will deviate in the opposite direction after exiting. Thus, the total deviation will be:
180∘
Hint: Consider how the particle's path changes when it exits the magnetic field and how this relates to the angle of deviation.
Step 5: Conclusion
The deviation of the particle from its original path after exiting the magnetic field is 180∘.
Final Answer: The particle will be deviated from its path by 180∘.
A charged particle enters a magnetic field perpendicularly, which means it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path is denoted as r.
According to the problem, the length of the magnetic field L is given as 1.5 times the radius of the circular path:
L=1.5×r
When the particle enters the magnetic field, it will begin to move in a circular path with radius r. The time it takes for the particle to complete a full circle is determined by its speed and the radius.
Since the length of the magnetic field L is 1.5r, the particle will not complete a full circular path. Instead, it will travel through the magnetic field and exit after covering a distance of 1.5r.
θ=1.52π×360∘=540∘2π≈86.6∘
180∘
The deviation of the particle from its original path after exiting the magnetic field is 180∘.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT Based Questions
Explore 20 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-V (SINGLE ANSWER QUESTION)
Explore 85 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level-II(C.W)
Explore 63 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
A charged particle enters a region of uniform magnetic field at an angle of 85∘ to the magnetic line of force . The path of the particle is a circle .
View SolutionA charged particle enters a magnetic field at an angle of 90∘with the magnetic field. The path of the particle will be a/an
View Solution
Knowledge Check
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Aincreases the K.E. of the particleBdecreases the K.E. of the particleCchanges the direction of motion of the particleDdoes both (a) and ( c)When a charged particle enters a uniform magnetic field its kinetic energy
Aremains constantBincreasedCdecreasesDbecomesA charged particle entering magnetic field obliquely will describe a path
AcircularBhelicalCparabolicDspiral
A β-particle enters a magnetic field making an angle of 45∘ with the field lines. The path of the particle is
View SolutionA charged particle entering a magnetic field from outside in a direction perpendicular to the field
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
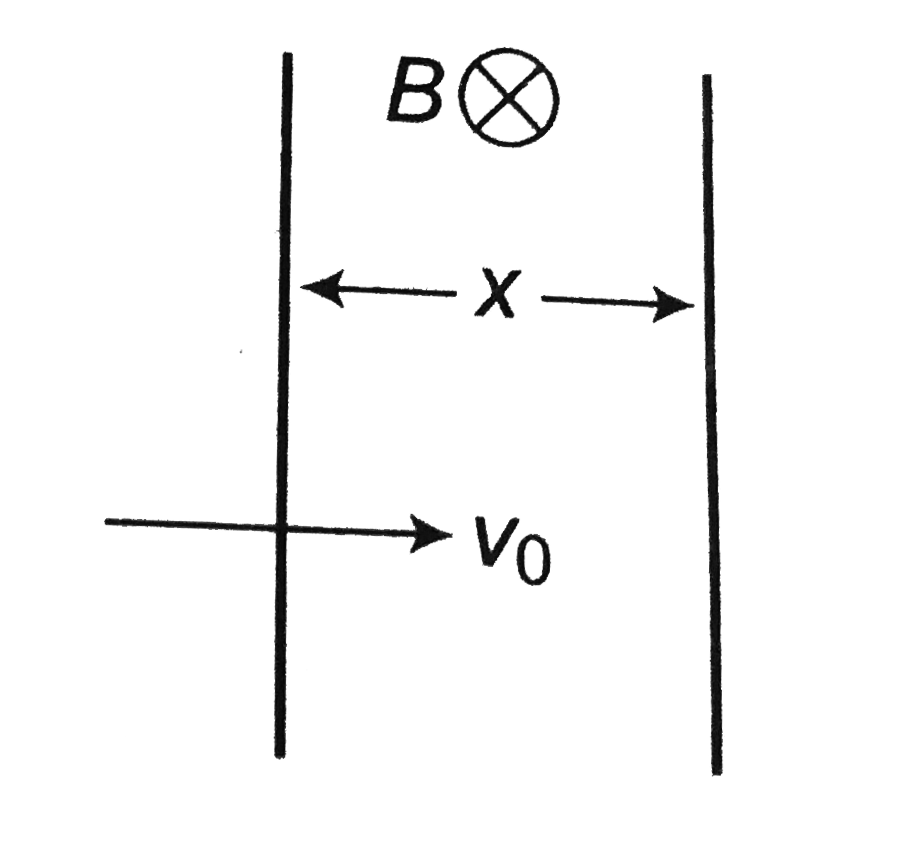
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of change in velocity of the particle when it comes out of the field is
View SolutionA proton, a deuteron and an o particle enter a magnetic field perpendicular to field with same velocity. What is the ratio of the radii of circular paths?
View Solution

