Renu purchases two bags of fertiliser of weights 75 kg and 69 kg. Find the maximum value of weight which can measure the weight of the fertiliser exact number of times.
To find the maximum value of weight that can measure the weights of the fertiliser (75 kg and 69 kg) an exact number of times, we need to calculate the Highest Common Factor (HCF) of the two weights. Here’s how to do it step by step:
Step 1: Find the prime factorization of each weight.
- For 75 kg:
- Divide 75 by the smallest prime number, which is 3:
- 75÷3=25
- Now, factor 25:
- 25÷5=5
- 5÷5=1
- So, the prime factorization of 75 is:
- 75=3×5×5=3×52
- For 69 kg:
- Divide 69 by the smallest prime number, which is 3:
- 69÷3=23
- Since 23 is a prime number, we stop here.
- So, the prime factorization of 69 is:
- 69=3×23
Step 2: Identify the common prime factors.
- The prime factors of 75 are 3,5,5 (or 3,52).
- The prime factors of 69 are 3,23.
- The common prime factor is 3.
Step 3: Calculate the HCF.
- The HCF is the product of the lowest powers of all common prime factors.
- Here, the only common prime factor is 3.
- Therefore, the HCF of 75 and 69 is:
- HCF=31=3
Step 4: Conclusion.
- The maximum value of weight that can measure the weights of the fertiliser (75 kg and 69 kg) an exact number of times is 3 kg.
- Divide 75 by the smallest prime number, which is 3:
- 75÷3=25
- Now, factor 25:
- 25÷5=5
- 5÷5=1
- So, the prime factorization of 75 is:
- 75=3×5×5=3×52
- Divide 69 by the smallest prime number, which is 3:
- 69÷3=23
- Since 23 is a prime number, we stop here.
- So, the prime factorization of 69 is:
- 69=3×23
- The prime factors of 69 are 3,23.
- The common prime factor is 3.
- Here, the only common prime factor is 3.
- Therefore, the HCF of 75 and 69 is:
- HCF=31=3
Topper's Solved these Questions
- PLAYING WITH NUMBERSBOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.2
11 Videos
- PLAYING WITH NUMBERSBOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.1
4 Videos
- PLAYING WITH NUMBERSBOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.5
12 Videos
- MENSURATIONBOOK - NCERTCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.2
1 Videos
- RATIO AND PROPORTIONBOOK - NCERTCHAPTER - RATIO AND PROPORTIONEXERCISE - SOLVED EXAMPLES
15 Videos
Similar Questions
Knowledge Check
The weight of 37 bags of sugar is 3644.5 kg. If all the bags weigh equally what is the weight of each bag ?
A98.5kgB96.5kgC80.5kgD90.5kgIf the weight of a man on the surface of the earth is 75kg, then his weight on the surface of the moon will be
A150 kg-wtB50 kg-wtC12.5 kg-wtD25 kg-wtTwo weights of 7 kg and 9 kg are hanging through the end-points of a light wire. The centre of mass of this system, from 7 kg weight, is at a distance of
A4.5 mB3.5 mC5.0mD3 m
Two bags of sugar contain 26 and 39 kg of sugar, respectively. What is the greatest weight that can be used to measure the weight in each bag an exact number of times ? How many times will it take to weight all the sugar in the two bags using this weight ?
View SolutionKiara weighs 34.5 kg. Her uncle weighs 69 kg more than Kiara's weight. What is their total weight?
View SolutionThe weight (in kg) of students are given below :
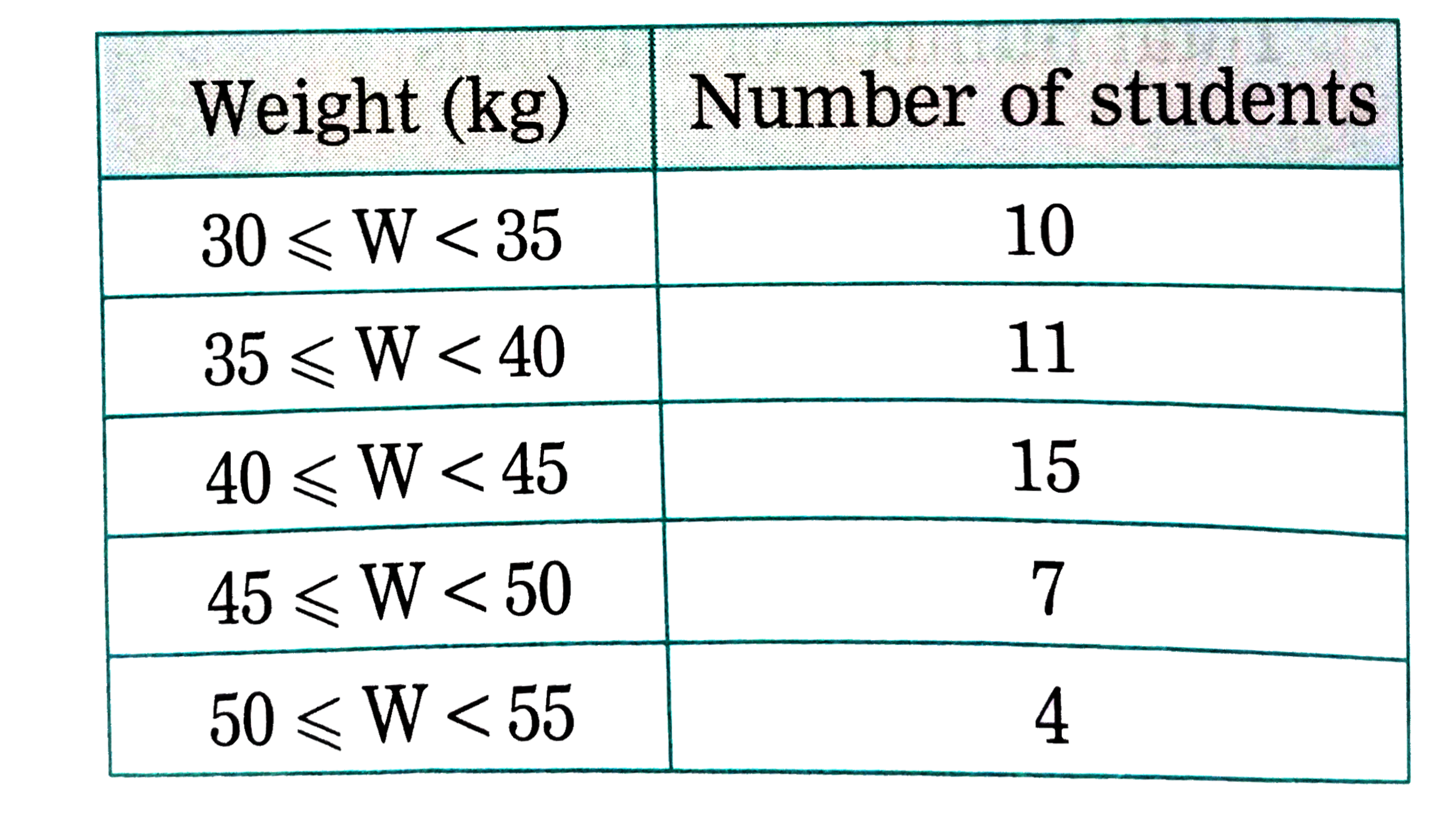
Find the median weight of a student.
View SolutionRani bought 6 bags of cement, each weighing 18 kg 300 g. Find the total weight of cement.
View SolutionThe mean weight of a class of 35 student is 45 kg. if the weight of the teacher be included, the mean weight increases by 500g. Find the weight of the teacher.
View Solution
