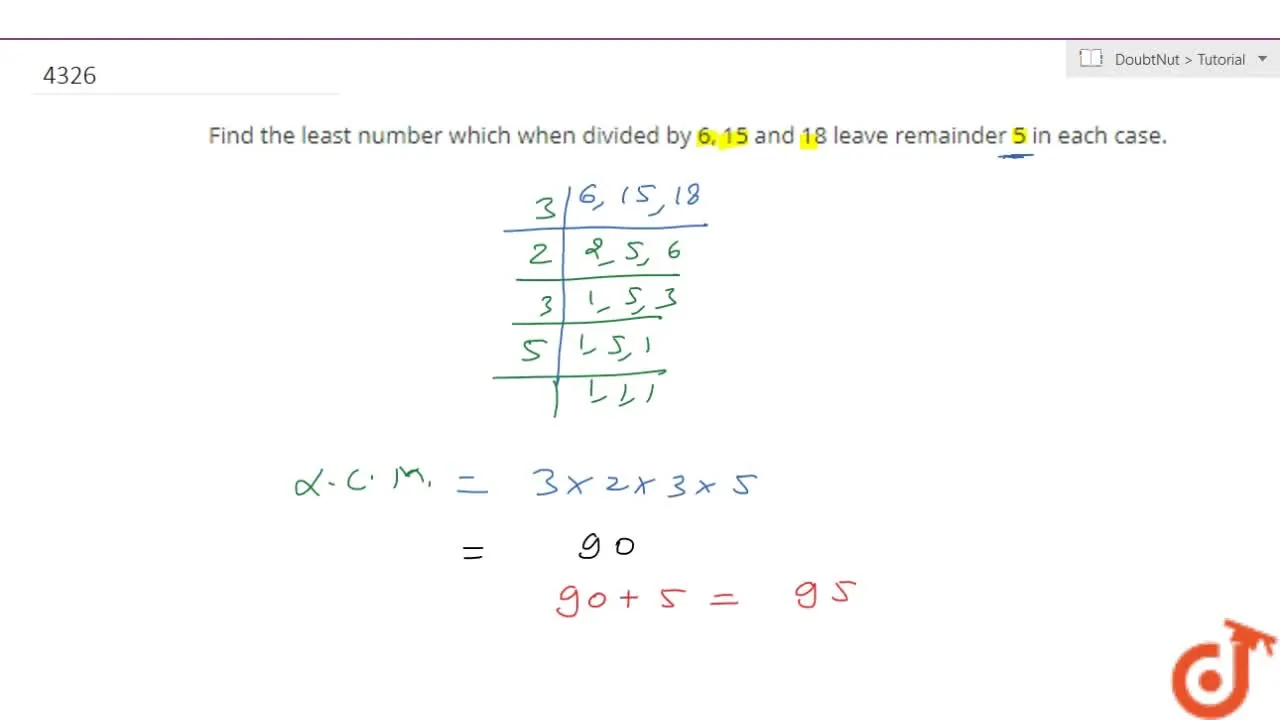Find the least number which when divided by 6, 15 and 18 leave remainder 5 in each case.
LCM(6,15,18)=2*3*3*5=90
adding remainder=90+5=95
Related Playlists
- BOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.211videos
PLAYING WITH NUMBERS
- BOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.14videos
PLAYING WITH NUMBERS
- BOOK - NCERTCHAPTER - PLAYING WITH NUMBERSEXERCISE - EXERCISE 3.512videos
PLAYING WITH NUMBERS
- BOOK - NCERTCHAPTER - MENSURATIONEXERCISE - EXERCISE 10.21videos
MENSURATION
- BOOK - NCERTCHAPTER - RATIO AND PROPORTIONEXERCISE - SOLVED EXAMPLES15videos
RATIO AND PROPORTION
Similar Questions
Find the least number which when divided by 16, 18 and 20 leaves a remainder 4 in each case, but is completely divisible by 7.
View SolutionFind the least number which when divided by 25, 40 and 60, leaves remainder 7 in each case.
View SolutionDetermine the least number which when divided by 3, 4 and 5 leaves remainder 2 in each case.
View SolutionFind the least number which when divided by 16,36 and 40 leaves 5 as remainder in each case.
View SolutionFind the least number which when dividded by 12, 16, 18, 30 leaves remainder 4 in each case but it is completely divisible by 7 ?
View SolutionLet x be the least number, which when divided by 5, 6, 7 and 8 leaves a remainder 3 in each case but when divided by 9 leaves remainder 0. The sum of digits of x is:
View SolutionLet x be the least numbers, which when divided by 5, 6, 7 and 8 leaves a remainder 3 in each case but when divided by 9 leaves no remainder. The sum of digits of x is
View SolutionThe least number which when divided by 12, 16 and 18 leaves 5 as remainder in each case. Find the number.
View SolutionFind the least number which when divided by 24, 30 and 54 leaves 5 as remainder in each case.
View SolutionFind the least number which when divided by 5,7 and 8 leaves 3 as the remainder in each case.
View Solution