Using the relation →B=μ0(→H+→M), show that Xm=μr−1. Solution in Tamil
→B=μ0(→H+→M)
But from equation xm=∣∣∣→M→H∣∣∣, in vector form →M=Xm→H
Hence, →B=μ0(Xm+1)→H⇒→B=μ→H
Where, μ=μ0(Xm+1)⇒Xm+1=μμ0=μr
⇒Xm=μr−1
Topper's Solved these Questions
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Book:FULL MARKSChapter:MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Exercise:TEXT EVALUATION SOLVED
Explore 15 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Book:FULL MARKSChapter:MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENT Exercise:TEXT EVALUATION SOLVED -SHORT ANSWER QUESTIONS
Explore 10 Videos
- ELECTROSTATICS Book:FULL MARKSChapter:ELECTROSTATICS Exercise:ADDITIONAL QUESTIONS SOLVED ( VII. NUMERICAL PROBLEMS )
Explore 5 Videos
- OPTICSBook:FULL MARKSChapter:OPTICSExercise:ADDITIONAL QUESITON - II ADDITIONAL PROBLEMS:
Explore 11 Videos
Similar Questions
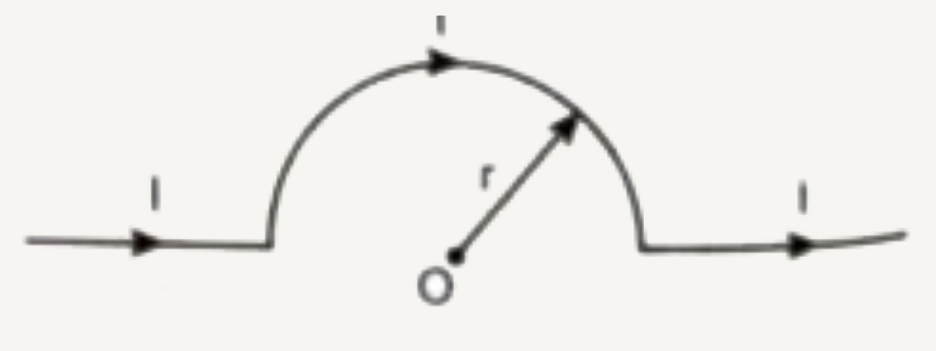
The magnetic field at the center O of the following current loop is ............ .
View SolutionWhat is meant by magnetic induction ?
View SolutionElectrons are caused to fall through a potential difference of 1500 volts. If they were initially at rest. Then calculate their final speed.
View SolutionLight from a point source in air falls on a spherical glass surface (n = 1.5 and radius of curvature = 20 cm ). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
View SolutionVectors vec m, vec n, vec r are such that vec m + vec n = vec r = 0 prov that vec m xxvec n = vec n xxvec r = vec r xxvec m
View Solutionif vec a=2vec m+vec n and vec b=vec m-2vec n angle between the vec m&vec n is 60^(@),a,b are side of the parallogram and |vec a|=1&|vec b|=1 then length of the diagonals:
View Solutionvec r xxvec a = vec b xxvec a, vec r xxvec b = vec a xxvec b, vec a! = 0, vec b! = 0, vec b! = lambdavec a, vec a is not perpendicular to vec b then vec r is
View SolutionA vector equation of the line of intersection of the planes vec r = vec b + lambda_ (1) (vec b-vec a) + mu_ (1) (vec a + vec c) vec r = vec c + lambda_ (2) (vec b-vec c) + mu_ (2) (vec a + vec b) and vec a, vec b, vec c being non coplanar vectors is
View SolutionPoynting vectors vec(S) is defined as vec(S)=(1)/(mu_(0))vec(E)xx vec(B) . The average value of 'vec(S)' over a single period 'T' is given by
View SolutionRelation between the magnetic field vector →B and magnetic intensity →H at a point in a magnetic field →B=μ→H where μ is the magnetic permeability of the medium in which the point is situated . Magnetic permeability of vacuum μ0=4π×10−7H.m−1 . Thus the relative magnetic permeability of the medium μr=μμ0 .
To define the magnetic field at a point in a medium another vector needs mention , which is magnetisation →M . The magnetic field is known as the magnetisation of the point . In most cases →M∝→H or, →M=k→H, this k is called the magnetic susceptibility of the medium . The relation among these vectors is expressed as →B=μ0(→H+→M).
Magnetic permeability at a point in the medium is 0.002H.m−1 . The magnetic susceptibility of the medium is
View SolutionRelation between the magnetic field vector →B and magnetic intensity →H at a point in a magnetic field →B=μ→H where μ is the mangnetic permeability of the medium in which the point is situated . Magnetic permeability of vacuum μ0=4π×10−7H.m−1 . Thus the relative magnetic permeability of the medium μr−μμ0 .
To define the magnetic field at a point in a medium another vector needs mention , which is magnetisation →M . The magnetic field is known as the magnetisation of the point . In most cases →M∝→H or, →M=k→H, this k is called the magnetic susceptibility of the medium . The relation among these vectors is expressed as →B=μ0(→H+→M).
Magnetisation at a point in the medium is 0.002A.m−1 . The intensity at the point is (inA.m−1 )
View SolutionRelation between the magnetic field vector →B and magnetic intensity →H at a point in a magnetic field →B=μ→H where μ is the mangnetic permeability of the medium in which the point is situated . Magnetic permeability of vacuum μ0=4π×10−7H.m−1 . Thus the relative magnetic permeability of the medium μr−μμ0 .
To define the magnetic field at a point in a medium another vector needs mention , which is magnetisation →M . The magnetic field is known as the magnetisation of the point . In most cases →M∝→H or, →M=k→H, this k is called the magnetic susceptibility of the medium . The relation among these vectors is expressed as →B=μ0(→H+→M).
Magnetic field at the same point (in Wb.m−2 )is
View SolutionThe maxwell’s equation :
∮→B.→dl=μ0(i+ɛ0.dϕEdt) is a statement of -
View SolutionIf →r.→a=0,→r.→b=1 and [→r→a→b]=1,→a.→b≠0,(→a.→b)2−|→a|2∣∣→b∣∣2=−1, then find →r in terms of →a and →b.
View SolutionIf →a×→b=→b×→c≠0 , then show that →a+→c=m→b, where m is any scalar.
View Solution