Construct the region represented by the inequations x+y≤3andx−y≤2.
Video Solution
Text Solution
(a) We first draw x+y=3.
⇒y=3−x
x031y302
Substitute (0, 0) in x−y≤2.
⇒0−0≤2
⇒0≤2, which is true.
∴ The side of which the origin lies is the graph of x−y≤2.
The region common to the two half planes is the graph of the system of inequations, which is shown as the shaded region in the figure below.
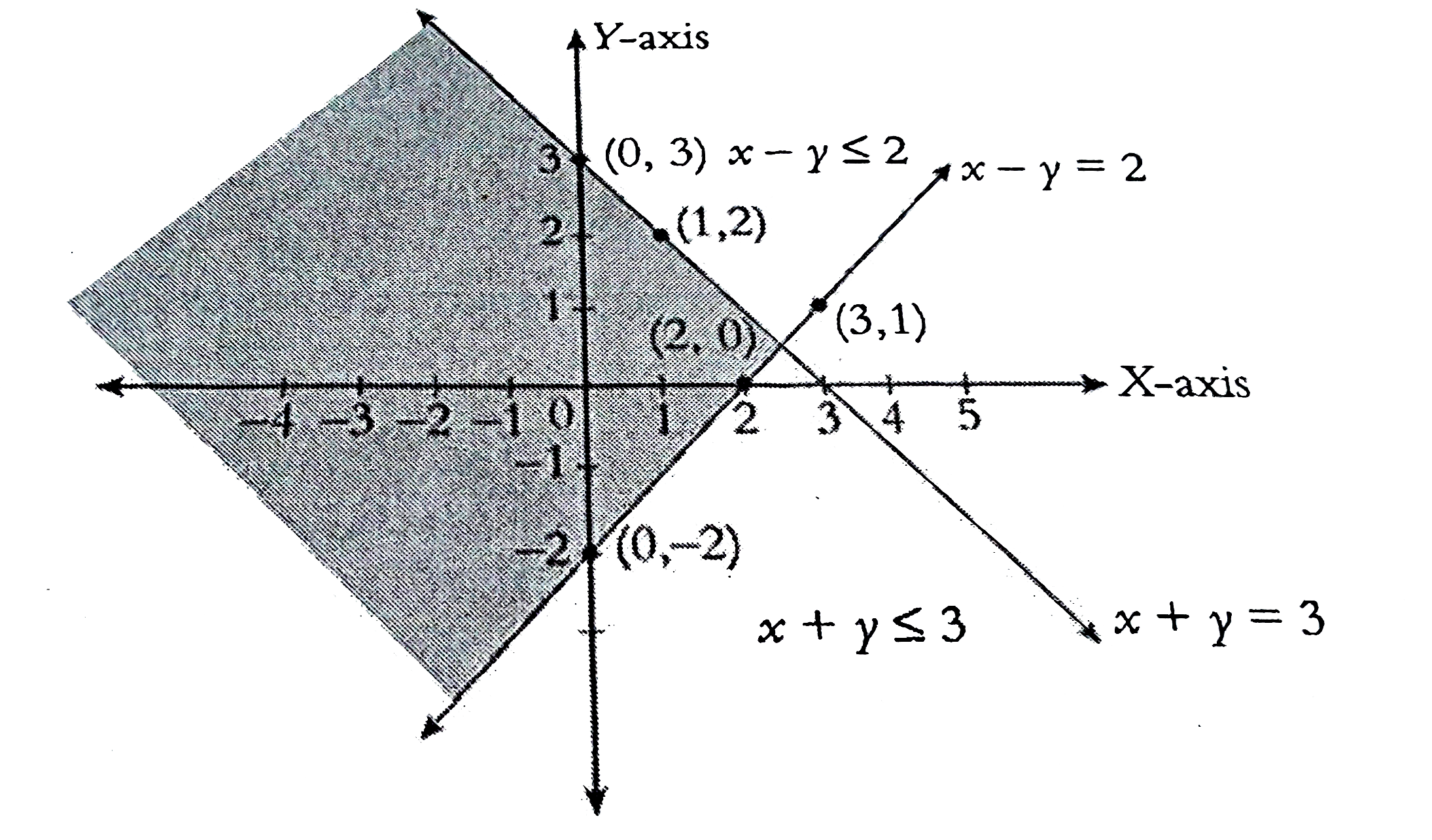
|
Topper's Solved these Questions
- LINEAR EQUATIONS AND INEQUATIONS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONS EXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
30 Videos
- LINEAR EQUATIONS AND INEQUATIONS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONS EXERCISE - SHORT ANSWER TYPE QUESTIONS
15 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
- MATRICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICES EXERCISE - Concept Application Level -2
15 Videos
Similar Questions
Knowledge Check
The region rprsented by the inequation system x,y≥0,y≤6,x+y≤3, is
Aunbounded in first quadrantBunbounded in first and second quadrantsCbounded in first quadrantDNone of the aboveThe region represented by 2x+y≥6 is
AboundedBunboundedCdoes not existDNone of theseThe total number of integral points i.e. points having integral coordinates lying in the region represented by the inequations |x−y|<3 and |x+y|<3 is
A25B36C13D12
Construct the region represented by the inequations x+y≥4and3x+2y≤6.
View SolutionConstruct the region represented by the inequations x+y≤3andx−y≤2.
View SolutionShade the region represented by the inequations. x+y≤3 and 3x−2y≥4.
View SolutionWhich of the following points belong to the region represented by the inequations 2x−3y≥5andx−2y≤3 ?
(a) (3, 0)
(b) (−4,−4)
(c) (3,−5)
(d) (2,−2)
(e) (5, 1)
View SolutionThe region represented by 2x+y≥6 is
View Solution