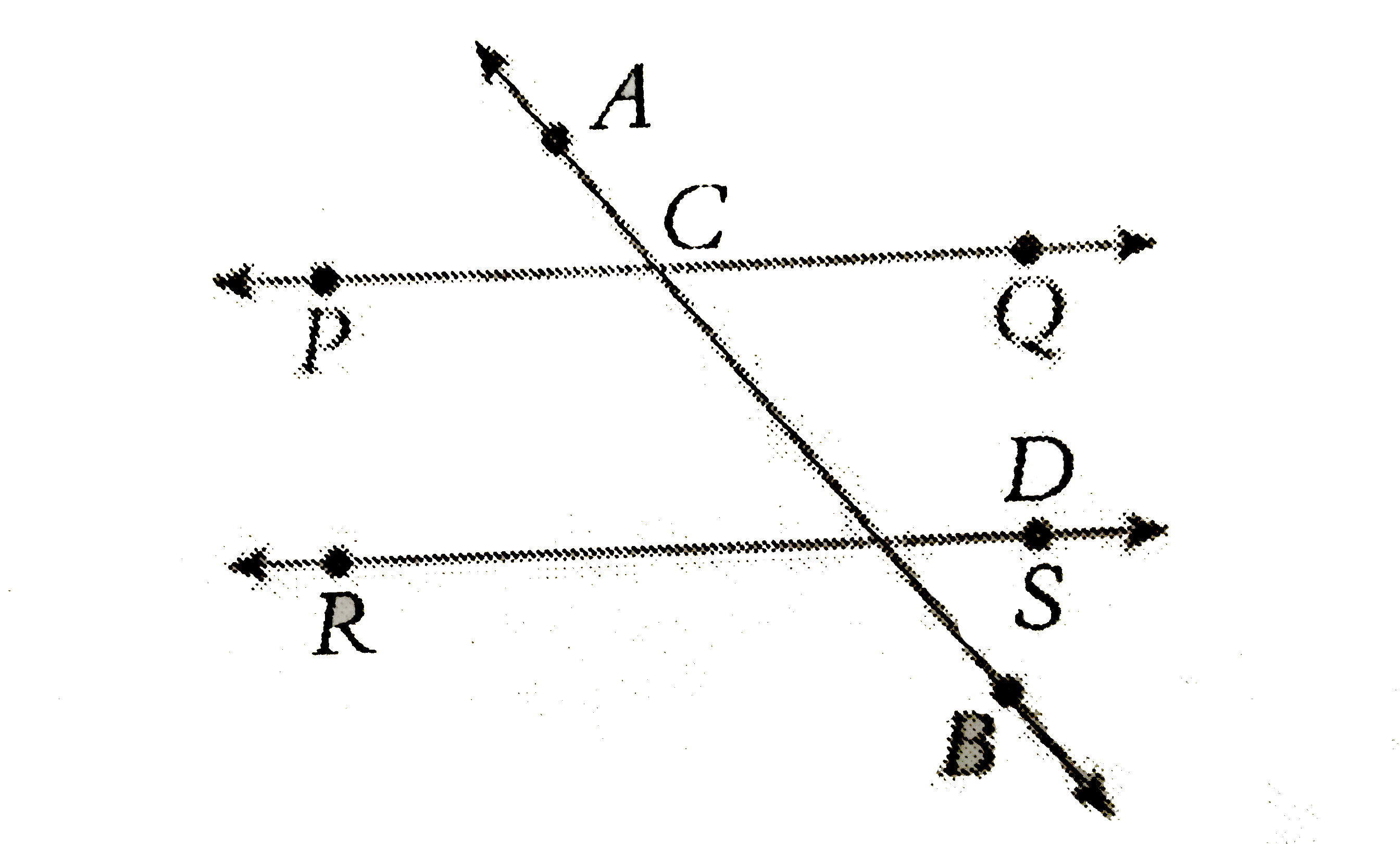
In the figure above, ¯¯¯¯¯¯PQand¯¯¯¯¯RS are parallel. ¯¯¯¯¯¯AC is transversal of ¯¯¯¯¯¯PQand¯¯¯¯¯RS. If ∠(ACP)=5x−70∘and∠BDR=4x+70∘, then find the value of x.
Given that, ¯¯¯¯¯¯PQ//¯¯¯¯¯RSand¯¯¯¯¯¯AB is a transversal.
Aslo given, ∠ACP=5x−70∘and∠BDR=4x+70∘.
∠ACP+∠BDR=180∘ (∴ Exterior angles on the same side of the transversal.)
⇒5x−70∘+4x70∘=180∘
⇒9x=180∘⇒x=20∘
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - very Short answer Type Question
25 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Short answer Type Question
29 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions

In the figure above ¯¯¯¯¯¯PQand¯¯¯¯¯RS are parallel .¯¯¯¯¯¯AB is a transversal of ¯¯¯¯¯¯PQand¯¯¯¯¯RS. If ∠ACP=5x−70∘and∠BDR=4x+70∘ , then find the value of x
View Solution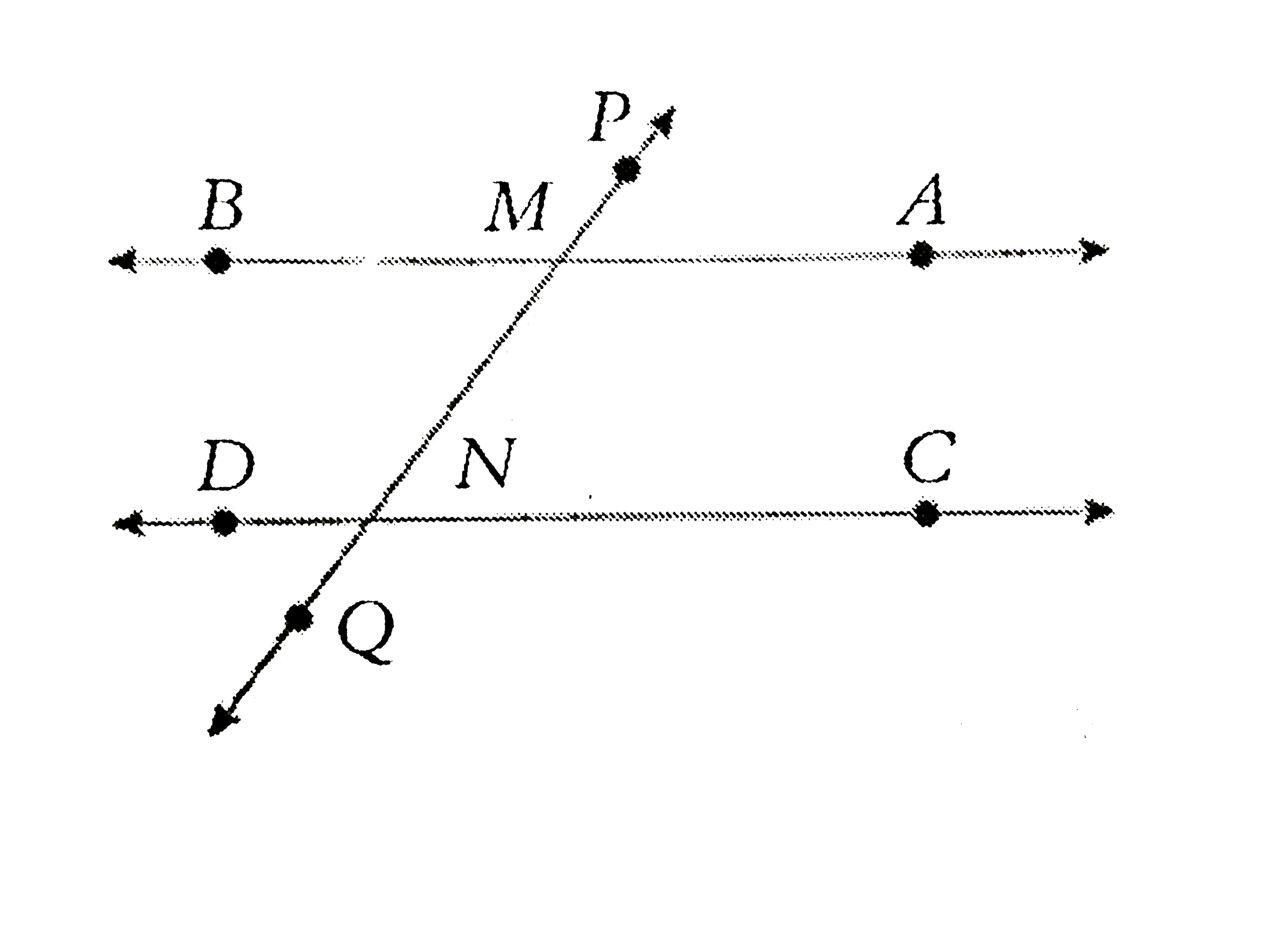
In the figure above, ¯¯¯¯¯¯BA is parallel to ¯¯¯¯¯¯DC, and ¯¯¯¯¯¯PQ is a transversal of ¯¯¯¯¯¯BAand¯¯¯¯¯¯DC. If ∠PMA=70∘and∠DNM=2x+30∘, then find the value of x.
View Solution
Knowledge Check

In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘

In the figure above, ¯¯¯¯¯¯BA is parallel to ¯¯¯¯¯¯DC, and ¯¯¯¯¯¯PQ is a transversal of ¯¯¯¯¯¯BAand¯¯¯¯¯¯DC. If ∠PMA=70∘and∠DNM=2x+30∘, then find the value of x.
View Solution
In the given figure, ¯¯¯¯¯¯¯LM//¯¯¯¯¯¯PN and the line l is a transversal of ¯¯¯¯¯¯¯LMand¯¯¯¯¯¯PN. Find the value of a .
View Solution
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.
View Solution
In the given figure, ¯¯¯¯¯¯¯LM//¯¯¯¯¯¯PN and the line l is a transversal of ¯¯¯¯¯¯¯LMand¯¯¯¯¯¯PN. Find the value of a .
View SolutionFind the value of 3.¯4×5.¯6
View SolutionIn the figure, ¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠ABC=110∘,∠ACD=30∘, then find ∠ADC.

View Solution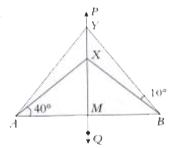
In the figure above ,¯¯¯¯¯¯PQ is the perpendicular bisector of ¯¯¯¯¯¯AB . If ∠XAB=40∘and∠XBY=10∘, then find ∠AYX
View Solution
