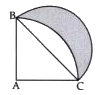
In the shown figure, two circles of radii of 7 cm each, are shown. ABCD is rectangle and AD and BC are the radii. Find the area of the shaded region (in cm2).

20
21
19
18
The correct Answer is:B
Required area is the difference of areas of rectangle and sum of areas sum of areas of two sectors.
Topper's Solved these Questions
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Level 2
20 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Level 3
21 Videos
- MENSURATIONBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MENSURATIONEXERCISE - Essay Type Questions
5 Videos
- MATRICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MATRICESEXERCISE - EXERCISE CONCEPT APPLICATION (LEVEL 3)
15 Videos
- MODULAR ARITHMETIC BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MODULAR ARITHMETIC EXERCISE - Level 3
15 Videos
Similar Questions
Knowledge Check
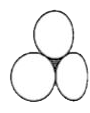
Three circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
 A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
In the given figure, ABCD is a square of side 7 cm. DPBA and DQBC are quardrants of circles each of the radius 7 cm. Find the area of the shaded region.

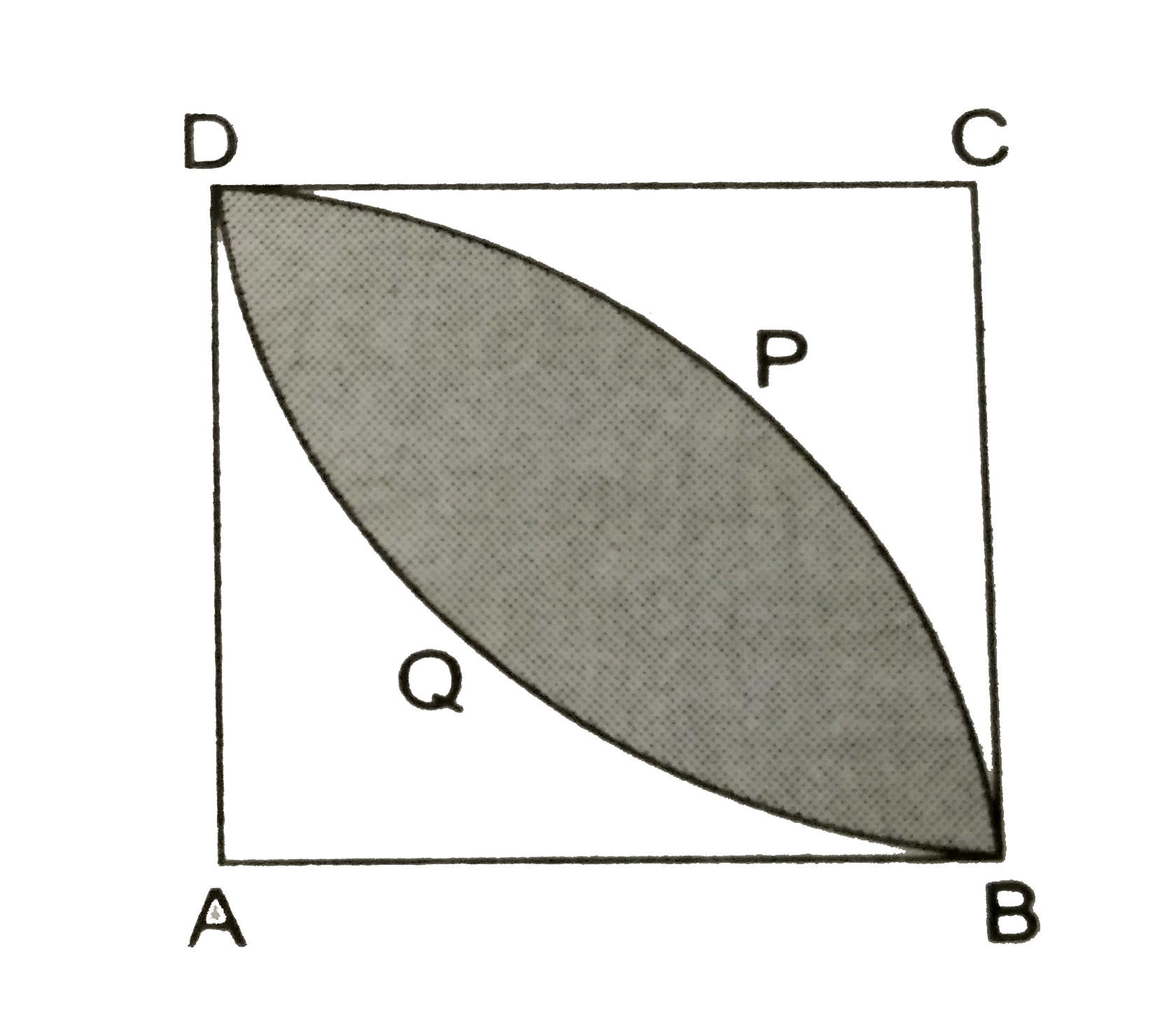
View SolutionIf □ABCD is a square, then the area of the shaded region shown in the figure is

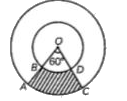
View SolutionIn the figure, the radii of two concentric circles with centre O are 7 cm and 14 cm and ∠AOC=60∘. Find the area of the shaded region.
View SolutionIn the figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
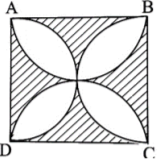
View SolutionIn the given figure, ABCD is a square of side 7cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.
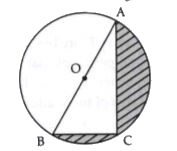
View SolutionIn figure , O is the centre of a circle such that diameter AB= 13 cm and AC = 12 cm . BC is joined .find the area of the shaded region .
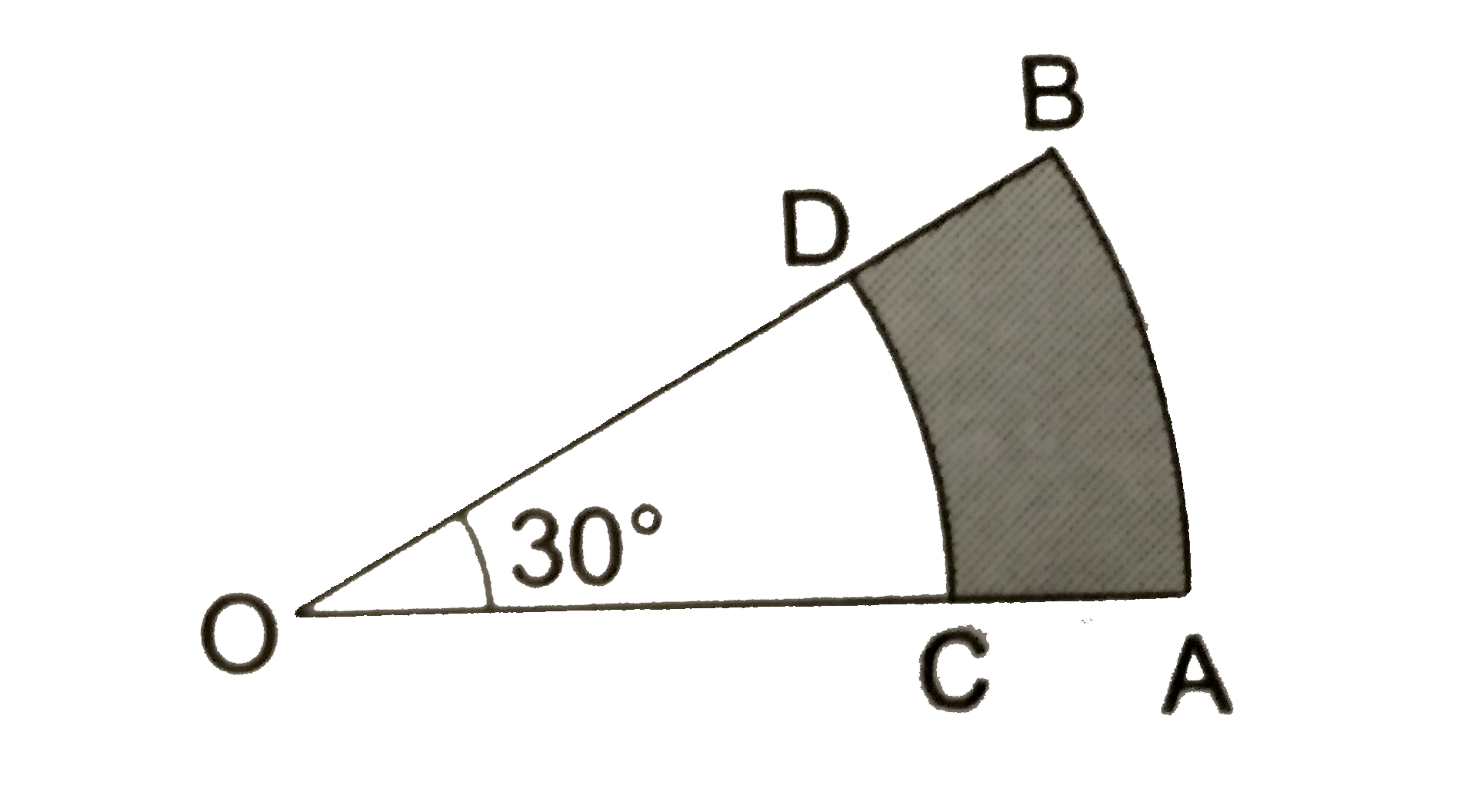
View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.
View Solution