किसी पतले लेंस से अपवर्तन के लिए सूत्र $\frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$ को स्थापित करें , जहाँ पदों के सामान्य अर्थ हैं।

Video Solution

Text Solution

Verified by Experts

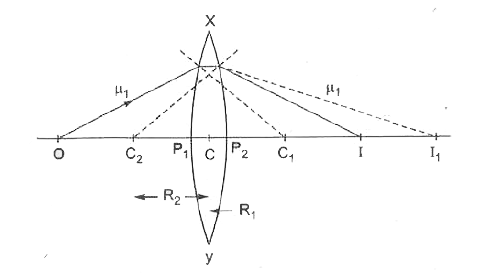
हम ऐसे लेंस पर विचार करते हैं जिसके पदार्थ का निरपेक्ष अपवर्तनांक $μ_{2}$ है। यह लेंस $μ_{1}$ निरपेक्ष अपवर्तनांक वाले माध्यम में स्थित है। $(μ_{1} < μ_{2})$ लैंस दो गोलीय अपवर्तक सतहों $X P_{1} Y$ एवं $X P_{2} Y$ से घिरा हुआ है। इन पृष्ठों का वक्रता केंद्र $C_{1}$ और $C_{2}$ तथा ,वक्रता त्रिज्याएँ $R_{1}$ और $R_{2}$ है। लेंस का प्रकाशिक केंद्र C है।
सतह $X P_{1} Y$ से अपवर्तन
$\frac{μ_{1}}{P_{1} O} + \frac{μ_{1}}{P_{1} C_{1}} = \frac{μ_{2}}{P_{1} C_{1}} - \frac{μ_{2}}{P_{1} I_{1}}$
$\Rightarrow \frac{μ_{1}}{P_{1} O} + \frac{μ_{1}}{R_{1}} = \frac{μ_{2}}{R_{1}} - \frac{μ_{1}}{P_{1} I_{1}} [∴ P_{1} C_{1} = R_{1}]$
$\Rightarrow \frac{μ_{1}}{P_{1} O} + \frac{μ_{2}}{P_{1} I_{1}} = \frac{μ_{2} - μ_{1}}{R_{1}}$

चूँकि लेंस बहुत पतला है इसलिए बिंदु लेंस $P_{1}$ के प्रकाशिक केंद्र C के बहुत निकट है।
$P_{1} O = C O$
$P_{1} I_{1} = C I_{1}$
$\Rightarrow \frac{μ_{1}}{C O} + \frac{μ_{2}}{C I_{1}} = \frac{μ_{2} - μ_{1}}{R_{1}}$
$X P_{2} Y$ सतह से अपवर्तन -
चूँकि वस्तु सघन माध्यम में स्थित है और प्रतिबिम्ब विरल माध्यम में बन रहा है।
$- \frac{μ_{2}}{P_{1} I_{1}} + \frac{μ_{2}}{P_{2} C_{1}} = \frac{- μ_{1}}{P_{2} I} + \frac{μ_{1}}{P_{2} C_{2}}$
$\Rightarrow - \frac{μ_{2}}{P_{2} I_{1}} + \frac{μ_{1}}{P_{2} I} = - \frac{(μ_{2} - μ_{1})}{R^{2}}$
चूँकि लेंस बहुत पतला है , इसलिए $P_{2}, C_{2}$ के बहुत निकट है।
$P_{2} I_{1} = C I_{1}$
$P_{2} I = C I$
$\Rightarrow - \frac{μ_{2}}{C l_{1}} + \frac{μ_{1}}{C I} = - \frac{(μ_{2} - μ_{1})}{R^{2}}$
समी (i) और (ii) को जोड़ने पर,
$\frac{μ_{1}}{C O} + \frac{μ_{1}}{C I} = (μ_{2} - μ_{1}) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
जहाँ $C O = - u, C I = + v$
$\Rightarrow - \frac{μ_{1}}{u} + \frac{μ_{1}}{v} = (μ_{2} - μ_{1}) [\frac{1}{R^{1}} - \frac{1}{R^{2}}]$
$\Rightarrow - \frac{1}{u} + \frac{1}{v} = (\frac{μ_{2}}{μ_{1}} - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$

यदि वस्तु अनन्त पर है तो प्रतिबिम्ब लेंस के मुख्य अक्ष पर बनता है अर्थात $u = \infty, v = f$
$\Rightarrow - \frac{1}{\infty} + \frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$
$\Rightarrow \frac{1}{f} = (\frac{μ_{2}}{μ_{1}} - 1) [\frac{1}{R_{1}} - \frac{1}{R_{2}}]$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION PAPER 2018

Topper's Solved these Questions

Similar Questions

JHARKHAND BOARD PREVIOUS YEAR PAPERS-QUESTION PAPER 2018-2018

Home
Ask Doubt
Profile