STATEMENT-1 The focla lengh of a lens does not depend on the medium in which it is submerged.
STATEMENT21f=μ2−μ1μ1(1R1−1R2)
STATEMENT -1is true statement 2 is true,Statement -2is a correct explanation for statement -1
STATEMENT -1is true statement 2 is true,Statement -2is a not a correct explanation for statement -1
Statement -1is true,Statement -2is False
Statement -1is False ,Statement -2is True
The correct Answer is:D
AS can be seen from the expression of f,it depends upon the refractive index of the medium which the lens is submerged.
Similar Questions
Statement-1 : A glass convex lens (refractive index, μ1=1.5), when immersed in a liquid of refractive index μ2=2, functions as a diverging lens.
Statement-2 : The focal length of a lens is given by 1f=(μ−1)(1R1−1R2), where μ is the relative refractive index of the material of the lens with respect to the surrounding medium.
View SolutionA point source of light is placed inside water and a thin converging lens ofrefractive index μ2 is placed just outside the plane surface of water. The image of the source is formed at a distance x from the surface of water. If the lens is now placed just inside water and the image is now formed at a distances' from the surface of water, show that
1x−1x1=μ1−1μ2−1×1f,
Where f is the focal length of the lens and μ1 is the refractive index of water.
View Solution
Knowledge Check
STATEMENT-1 The power of a thin lens does not depend upon the surrounding medium
STATEMENT2 power of a thin lensASTATEMENT -1is true statement 2 is true,Statement -2is a correct explanation for statement -1BSTATEMENT -1is true statement 2 is true,Statement -2is a not a correct explanation for statement -1CStatement -1is true,Statement -2is FalseDStatement -1is False ,Statement -2is TrueAssertion : A double convex lens (μ=1.5) has focal length 10cm. When the lens is immersed in water (μ=4/3) its focal length becomes 40cm.
Reason : 1f=μ1−μmμm(1R1−1R2)AIf both the assertion and reason are true and reason explains the assertion.BIf both the assertion and reason are true but reason does not explain the assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.STATEMENT-1 Power of a lens depends on nature of material of lens, medium in which it is placed and radii of curvature of its surface.
STATEMENT2 it follows the relationp=1f=(μ2μ1−1)[1R1−1R2]ASTATEMENT -1is true statement 2 is true,Statement -2is a correct explanation for statement -1BSTATEMENT -1is true statement 2 is true,Statement -2is a not a correct explanation for statement -1CStatement -1is true,Statement -2is FalseDStatement -1is False ,Statement -2is True
Two transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]
View SolutionSTATEMENT-1 Air bubble in glass medium behaves as concave lens.
STATEMENT2Lens formula is 1f=(μlensμmed−1)[1R1−1R2]
View SolutionStatement-1 : Focal length of an equiconvex lens of μ=3/2 is equal to radius of curvature of each surface.
Statement-2 : it follows from
1f=(μ−1)(1R1−1R2)
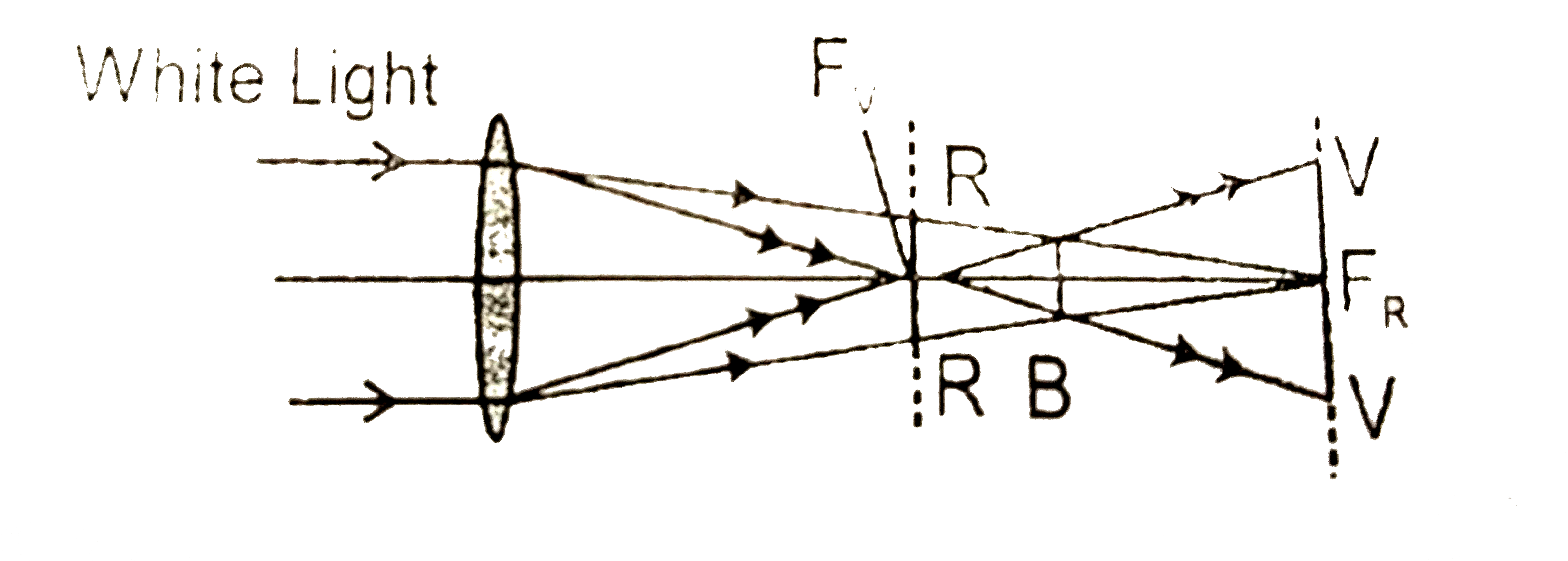
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
The dispersive power of crown and fint glasses are 0.02 and 0.04 respectively. An achromtic converging lens of focal length 40cm is made by keeping two lenses, one of crown glass and the other of flint glass, in contact with each other. The focal lengths of the two lenses are :
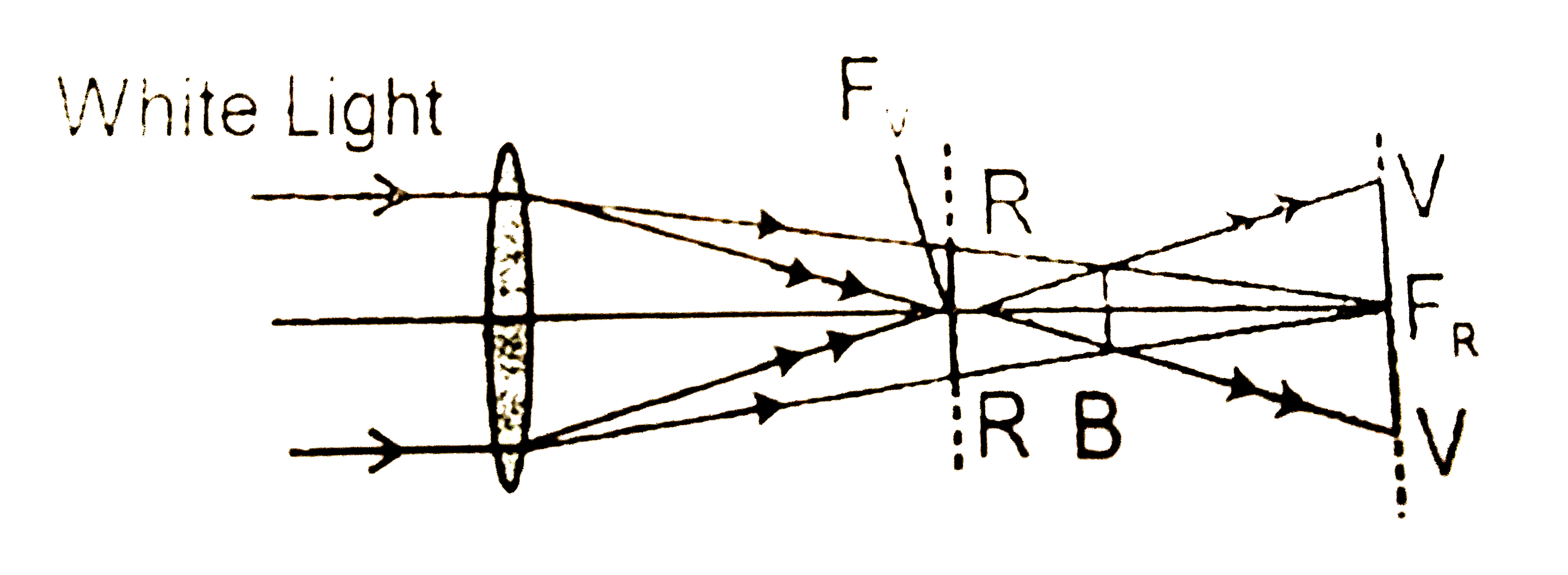
View SolutionThe image of a white object in with light formed by a lens is usually colored and blurred. This defect of image is called chromatic aberration and arises due to the fact that focal length of a lens is different for different colours. As R .I. μ of lens is maximum for violet while minimum for red, violet is focused nearest to the lens while red farthest from it as shown in figure.
As a result of this, in case of convergent lens if a screen is placed at Fv center of the image will be violet and focused while sides are red and blurred. While at FR , reverse is the case, i.e ., center will be red and focused while sides violet and blurred. The differece between fv and fR is a measure of the longitudinal chromatic aberration (L.C.A),i.e.,
L.C.A.=fR−fv=−df with df=fv−fR ...........(1)
However, as for a single lens,
1f=(μ−1)[1R1−1R2] .............(2)
⇒−dff2=dμ[1R1−1R2] ...............(3)
Dividing E1n. (3) by (2) :
−dff=dμ(μ−1)=ω,[ω=dμ(μ−1)]dispersive power,.........(4)
And hence, from Eqns. (1) and (4) ,
L.C.A.=−df=ωf
Now, as for a single lens neither f nor ω zero, we cannot have a single lens free from chromatic aberration.
Condition of Achromatism :
In case of two thin lenses in contact
1F=1F1+1F2i.c,.−dFF2=df1f21−df2f22
The combination will be free from chromatic aberration if dF=0
i.e.,df1f21+df2f22=0 which with the help of Eqn. (4) reduces to
ω1f1f21+ω2f2f22=0,i.e.,ω1f1+ω2f2=0........(5)
This condition is called condition of achromatism (for two thin lenses in contact ) and the lens combination which satisfies this condition is called achromatic lems, from this condition, i.e., form Eqn. (5) it is clear the in case of achromatic doublet :
Since, if ω1=ω2,1f1+1f2=0i.e.,1F=0 or F=∞
i.e., combination will not behave as a lens, but as a plane glass plate.
(2) As ω1 and ω2 are positive quantities, for equation (5) to hold, f1 and f2 must be of opposite nature, i.e., if one of the lenses is converging the other must be diverging.
(3) If the achromatic combination is convergent,
fC<fD and as fCfd=ωCωD,ωC<ωd
i.e., in a convergent achromatic doublet, convex lens has lesses focal legth and dispersive power than the divergent one.
A combination is made of two lenses of focal lengths f and f' in contact , the dispersive powers of the materials of the lenses are ω and ω' . The combination is achromatic when :
View Solution

