Doubtnut Promotions Sticky

∣∣∣Z1−1Z1−4∣∣∣=2&∣∣∣Z2−4Z2−1∣∣∣=2 the |Z1−Z2|max−|Z1+Z1|min = ?

A

2

B

3

C

5

D

10

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

z1 lies on the circle (x−1)2+y2=4((x−4)2+y2)⇒x2+y2−10x+21=0
z2 lies on the circle (x−4)2+y2=4((x−1)2+y2)⇒x2+y2=4
|z1−z2|min=1, (when z1=3 and z2=2)
|z1−z2|max=9 (when z1=7 and z2=−2)
∴|z1−z2|min+|z1−z2|max=10.
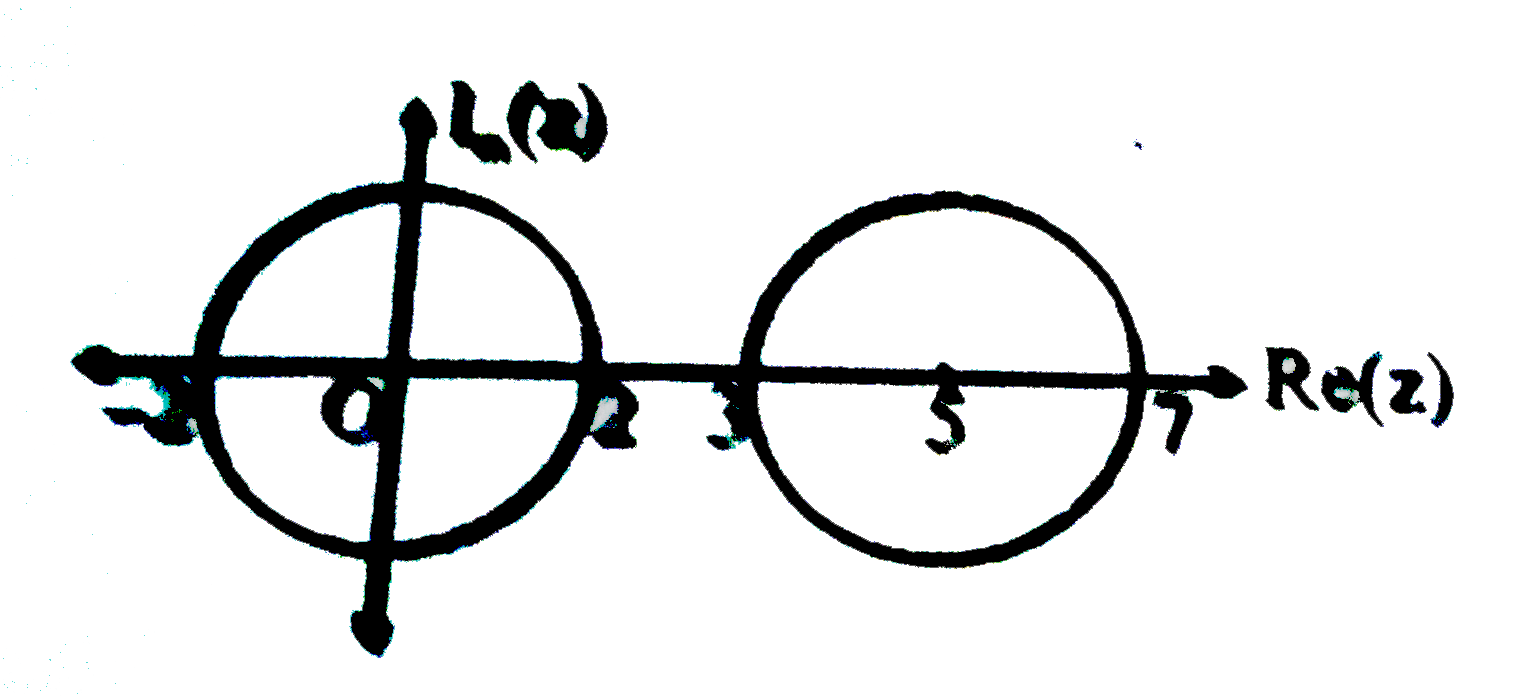
ocr_image

|
Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    If ∣∣∣z1z−z2z1z+z2∣∣∣=k,(z1,z2≠0) then

    Afor k=1 locus of z is straight line
    Bfor k cancel(in) {1,0}z lies on a circle
    Cfor k=0 z represents a point
    Dfor k=1,z lies on the perpendicular bisector of the segment joining z2z1andz2z1
  • Question 2 - Select One

    If PandQ are represented by the complex numbers z1andz2 such that ∣∣∣1z2+1z1∣∣∣=∣∣∣1z2−1z1∣∣∣, then the circumstance of ΔOPQ (where O is the origin) is

    A12(z1−z2)
    B13(z1+z2)
    C12(z1+z2)
    D13(z1−z2)
  • Question 3 - Select One

    If z1,z2,z3 are complex numbers such that |z1|=|z2|=|z3|=∣∣∣1z1+1z2+1z3∣∣∣=1, then [(1+i)n1+(1−i)n1]+[(1+i)n2+(1−i)n2] is

    Aequal to 1
    Bless than one
    Cgreater than 3
    Dequal to 3