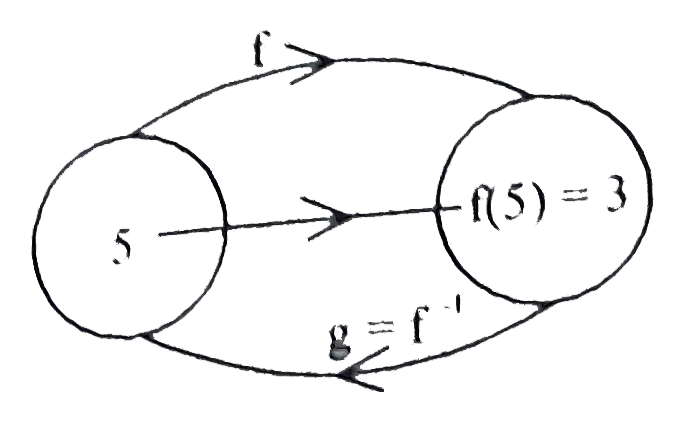
Suppose g is the inverse fiunction of a diffdifferentiable finction fa

Let g be the inverse function of a differentiable function f and $G (x) = \frac{1}{g (x)} .$ If $f (4) = 2$ and $f' (4) = \frac{1}{16},$ then the value of ${(G' (2))}^{2}$ equals to:
A1
B4
C16
D64
Let $g$ be the inverse function of $f and f' (x) = \frac{x^{10}}{1 + x^{2}} .$ If $g (2) = a$ then $g' (2)$ is equal to
A $\frac{5}{2^{10}}$
B $\frac{1 + a^{2}}{a^{10}}$
C $\frac{a^{10}}{1 + a^{2}}$
D $\frac{1 + a^{10}}{a^{2}}$
Let $g (x) = x^{3} - 4 x + 6 .$ If $f' (x) = g (x) and f (1) = 2,$ then what is f(x) equal to?
A $x^{3} - 4 x + 3$
B $x^{3} - 4 x + 6$
C $x^{3} - 4 x + 1$
D $x^{3} - 4 x + 5$

Suppose g is the inverse fiunction of a diffdifferentiable finction fand $G (x) = \frac{- 4}{g^{2} (x)} .$ If $f (5) = 3 and f' (5) = \frac{1}{125}$ then $g; (3)$ is equal to