Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R,. If f(−3)=2 and f(5)=4 in [−5,5] , then the equation f(x)=0 has
exactly 2 real roots.
exactly 3 real roots.
atleast 3 real roots.
atleast 5 real roots.
The correct Answer is:A
Given f(x)=−f(−x) in [−5,5]
⇒ f(x) is an odd function.
Since points (-3,2), (-1,-3) and (5,4) lies on the curve.
So, (3,-2), (1,3) and (-5,-4) will also lies on the curve.
For minimun number of roots, one of the possible graph of continuous function f(x) is as follows.
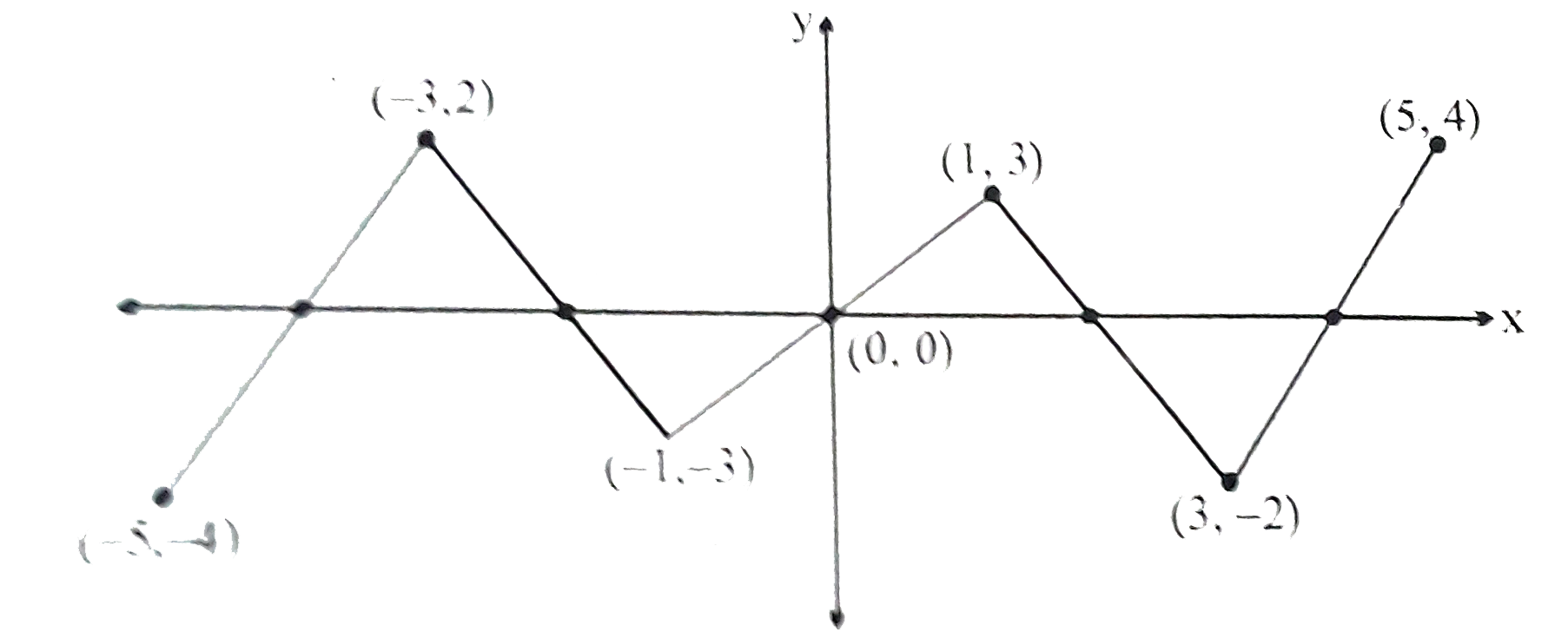
⇒ f(x)=0 has atleast 5 solutions.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION - 2 PART A [PARAGRAPH TYPE]6videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - MATHS SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]6videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - CHEMISTRY SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]6videos
TEST PAPERS
- BOOK - BANSALCHAPTER - PROBABILITYEXERCISE - All Questions1videos
PROBABILITY
- BOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Match the column7videos
THERMODYNAMICS
Similar Questions
Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R,. If f(−3)=2 and f(5)=4 in [−5,5] , then the equation f(x)=0 has
View SolutionLet f:R→R be a continuous onto function satisfying f(x)+f(−x)=0∀x∈R. If f(−3)=2andf(5)=4∈[−5,5], then the minimum number of roots of the equation f(x)=0 is
View Solution
Knowledge Check
- Question 1 - Select One or More
Let f(x) be a function satisfying f(x)f(x+2)=10∀x∈R, then
Af(x) is a periodic functionBf(x) is aperiodic functionC7∫1f(x)dx=20D7∫1f(x)dx=20 - Question 2 - Select One or More
Let f be a differentiable function satisfying f'(x)=f'(−x)∀x∈R. Then
AIf f(1)=f(2), then f(−1)=f(−2)B12f(x)+12f(y)=f(12(x+y))) for all ral values of x,yCLet f(x) be an even function, then f(x)=0∀x∈RDf(x)+f(−x)=2f(o)∀x∈R
Let f:R→R be a continuous onto function satisfying f(x)+f(−x)=0,∀x∈R . If f(−3)=2andf(5)=4 in [-5, 5], then what is the minimum number of roots of the equation f(x) = 0?
View Solutionf:R→R;f(x) is continuous function satisfying f(x)+f(x2)=2∀x∈R, then f(x) is
View Solutionf:R→R;f(x) is continuous function satisfying f(x)+f(x2)=2∀x∈R, then f(x) is
View SolutionLet f:R→R be a function satisfying 3f(x)+2f(−x)=x2−x∀x∈R then f(x) is
View SolutionLet f:R→R be a function satisfying 3f(x)+2f(−x)=x2−x∀x∈R ,then f(x) is
View SolutionLet f be a continuous function on R satisfying f(x+y) =f(x)f(y) for all x, y ∈ R and f(1)=4 then f(3) is equal to
View Solution

