A man of height 1.7 m walks at a uniform speed of 6.6 m/min from a lamp post which is 5m high.Find the rate at which the length of his shadow increases.

Video Solution

Text Solution

Verified by Experts

Let AB is a lamp post of height 5 m. Let at any time 't', a man of height 1. 7 m is at a distance 'y' metre from the lamp post and its shadow is CE = x metre.
Let $∠ C E D = θ$
$I n Δ C E D,$
$tan θ = \frac{C D}{C E}$

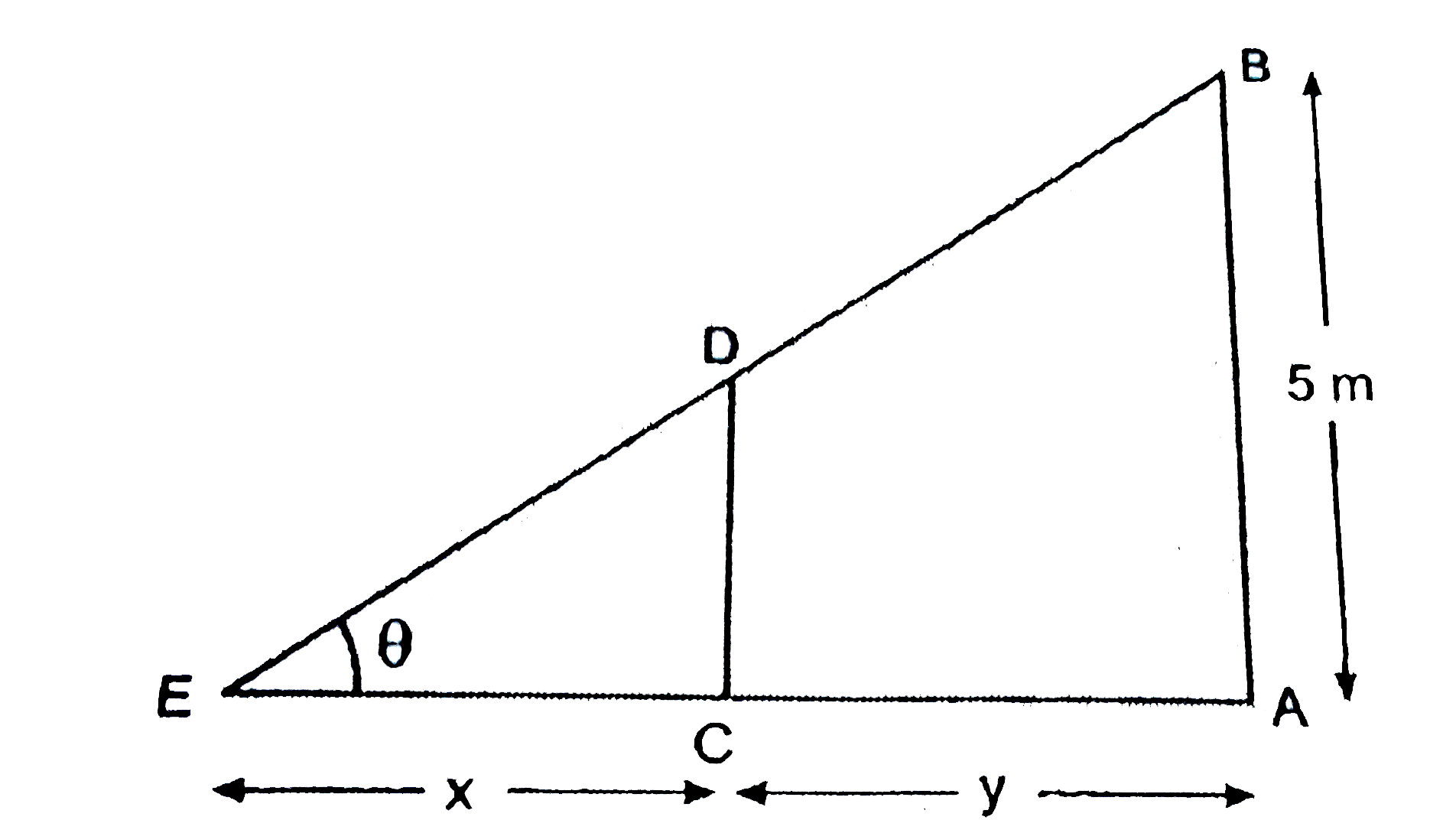
And in $Δ A B E,$
$tan θ = \frac{A B}{A E}$
$∴ \frac{C D}{C E} = \frac{A B}{A E}$
$\Rightarrow \frac{1.7}{x} = \frac{5}{x + y}$
$\Rightarrow 5 x = 1.7 x + 1.7 y$
$\Rightarrow 3.3 x = 1.7 y$
$\Rightarrow x = \frac{17}{33} y$
$∴ \frac{d x}{d t} = \frac{17}{33} \times \frac{d y}{d t}$
$= \frac{17}{33} \times 6.6 = 3.4 m / min .$
Therefore the shadow is increasing at the rate of 3.4 m/min.

Updated on:21/07/2023