If the eccentric angles of two points P and Q on the ellipse x228+y27=1 whose centre is C differ by a right angle then the area of ΔCPQ is
A
5
B
6
C
7
D
8
Video Solution
Text Solution
The correct Answer is:C
If P is the point (acosθ,bsinθ), the coordinates of Q are (acos(θ+π2),bsin(θ+π2))
i.e., (−asinθ,bcosθ) where a2=28,b2=7
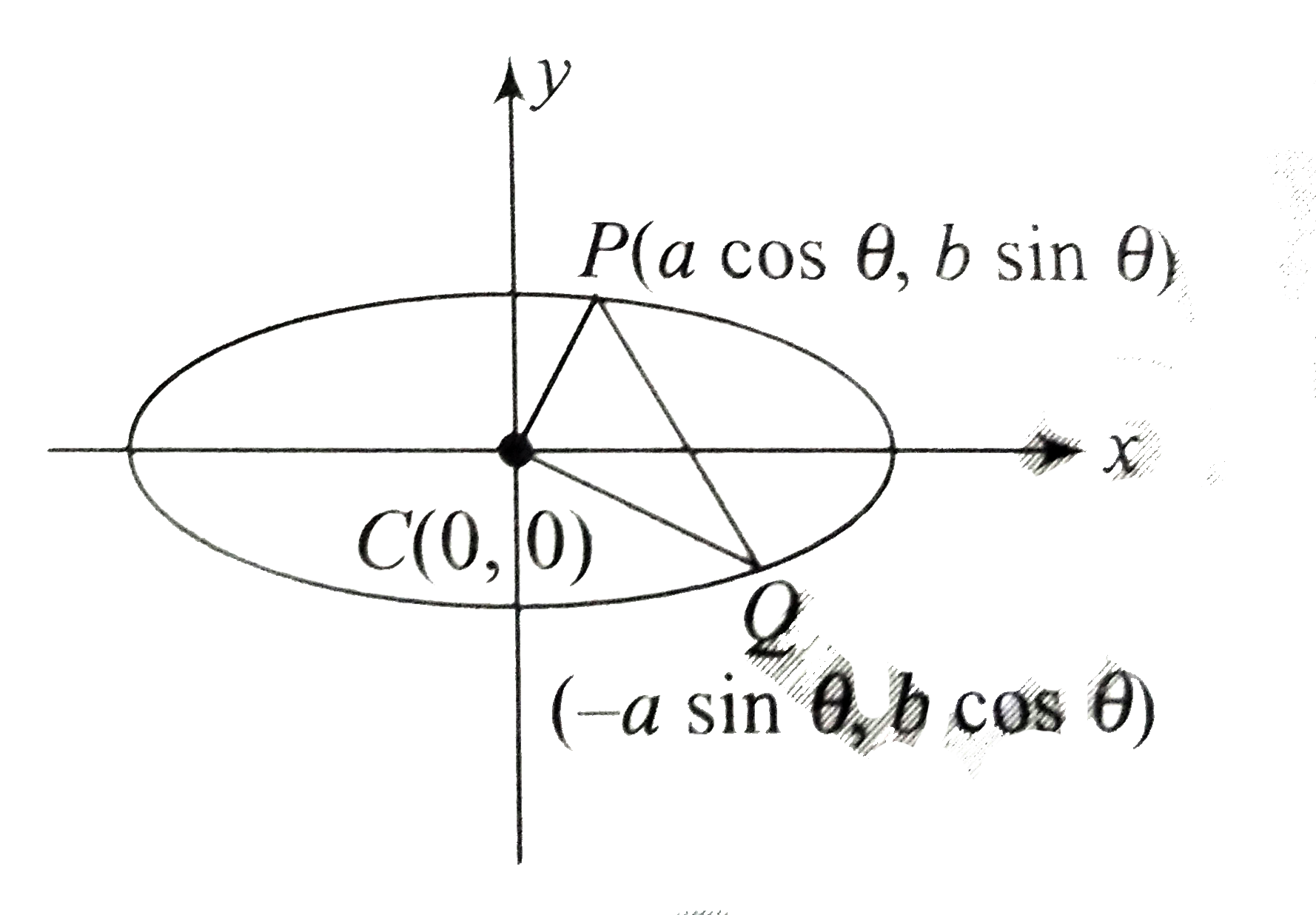
∴ The area of ΔCPQ=12∣∣abcos2θ+absin2θ∣∣{∵area=∣∣∣{12(x1y2−x2y2)}∣∣∣}
=12ab
=12(√28)(√7)=7 sq units.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the eccentric angles of two points P and Q on the ellipse x2a2+y2b2 are α,β such that α+β=π2, then the locus of the point of intersection of the normals at P and Q is
Aax+by=0Bax-by=0Cx+y=0Dx+y=a+bThe eccentric angle of a point on the ellipse x26+y22=1 whose distance from the centre of the ellipse is 2, is
A210∘B270∘C300∘D45∘The ecentric angle of the points on the ellipse x26+y22=1 whose distane from its centre is 2 is/are.
Aπ4B3π4C5π4D7π4
αandβ are eccentric angles of two points A and B on the ellipse x2a2+y2b2=1 If P (acosθ,bsinθ) be any point on the same ellipse such that the area of triangle PAB is maximum then prove that θ=α+β2
View SolutionFind the eccentric angle of a point on the ellipse x26+y22=1 whose distance from the center of the ellipse is √5
View SolutionFind the eccentric angle of a point on the ellipse x2+3y2=6 at a distance 2 units from the centre of the ellipse.
View SolutionThe eccentric angle of a point on the ellipse x26+y22=1 whose distance from the centre of the ellipse is 2, is
View SolutionP and Q are two points on the ellipse x2a2+y2b2=1 whose eccentric angles are differ by 90∘, then
View Solution
