Consider two circles . Let be formed by the common tangents to circles , Then which of the following hold(s) good?
Incentre of is (1,0)
The equation of radical axis of circles and is
Product of slope of direct common tangents is
If transverse common tangent intersects direct common tangents at points A and B, then AB equals 4.
The correct Answer is:A, D
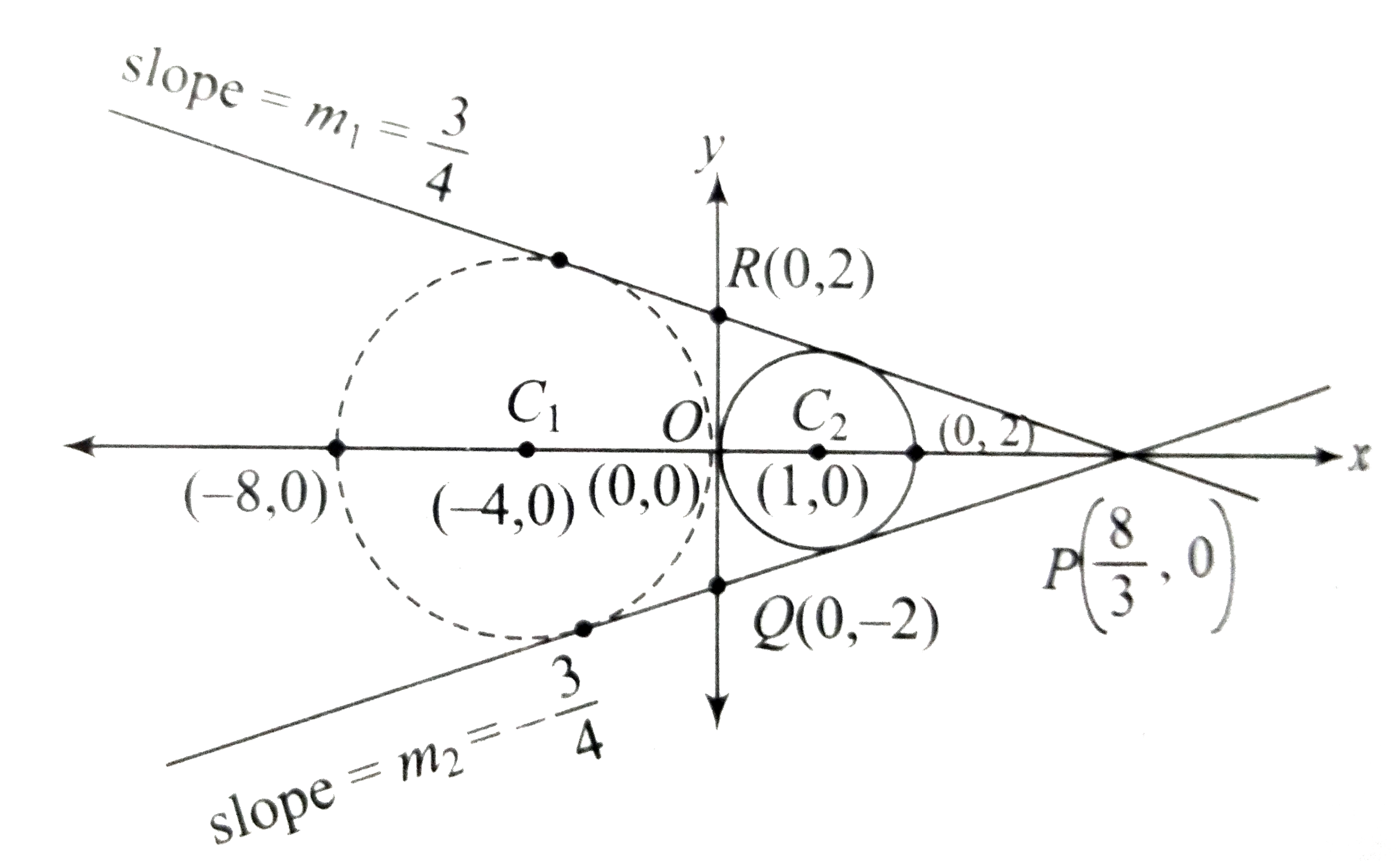
We have with centre and radius .
Also, we have with centre (1,0) and radius =1,
Hence, circles and touch each other externally. Also,
(As P divides the line segment joining the centres in a ratio of the radii externally)
Let equation of the direct common tangent by By applying condition of tangency, we get
or
Topper's Solved these Questions
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Single Correct Answer Type
Explore 58 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:JEE Advanced (Single Correct Answer Type)
Explore 14 Videos
- COMPLEX NUMBERSBook:CENGAGEChapter:COMPLEX NUMBERSExercise:Question Bank
Explore 30 Videos
Similar Questions
Knowledge Check
Consider the circles x2+y2=1 & x2+y2–2x–6y+6=0. Then equation of a common tangent to the two circles is
A4x – 3y – 5 = 0Bx + 1 = 0C3x + 4y – 5 = 0Dy – 1 = 0Consider the circles
S1:x2+y2−4x−6y−12=0
and S2:x2+y2+6x+18y+26=0
then which of the following is (are) correct?AThe circles S1 and S2 touches each other.BNumber of common tangent(s) to S1 and S2 is 1.CThe equation of radical axis of S1 and S2 is 5x+12y+19=0.DCircle S2 neither touches nor cuts the coordinate axes.Let S1={x∣x is th ratio of circumference and diametr of circle},S2={π}, then which of the following is incorrect ?
AS1−S2=ϕBS1∪S2=S1CS1=S2DNone of these
Consider two circles S1=x2+(y−1)2=9 and S2=(x−3)2+(y−1)2=9 , now for these circles match the following :

View SolutionFor the circles S1:x2+y2−4x−6y−12=0 and S2:x2+y2+6x+4y−12=0 and the line L.:x+y=0 (A) L is common tangent of S1 and S2 (B) L is common chord of S1 and S2 (C) L is radical axis of S1 and S2 (D) L is perpendicular to the line joining the cente of S1 & S2
View SolutionThe common tangents to the circles x2+y2+2x=0andx2+y2−6x=0 form a triangle which is
View SolutionThe angle between the circles
S: x2+y2−4x+6y+11=0 and S':x2+y2−2x+8y+13=0 is
View SolutionThe common tangents to the circles x2+y2+2x=0 and x2+y2−6x=0 from a triangle which is :
View Solution