Line $3 x + b y = k$ intersect the curve $2 x^{2} + 3 y^{2} + 2 x y = 1$ at points A and B. Thecircle on AB as diameter passes through origin,then sum of all possible values of 'k' is

A

3

B

4

C

$- 4$

D

$- 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

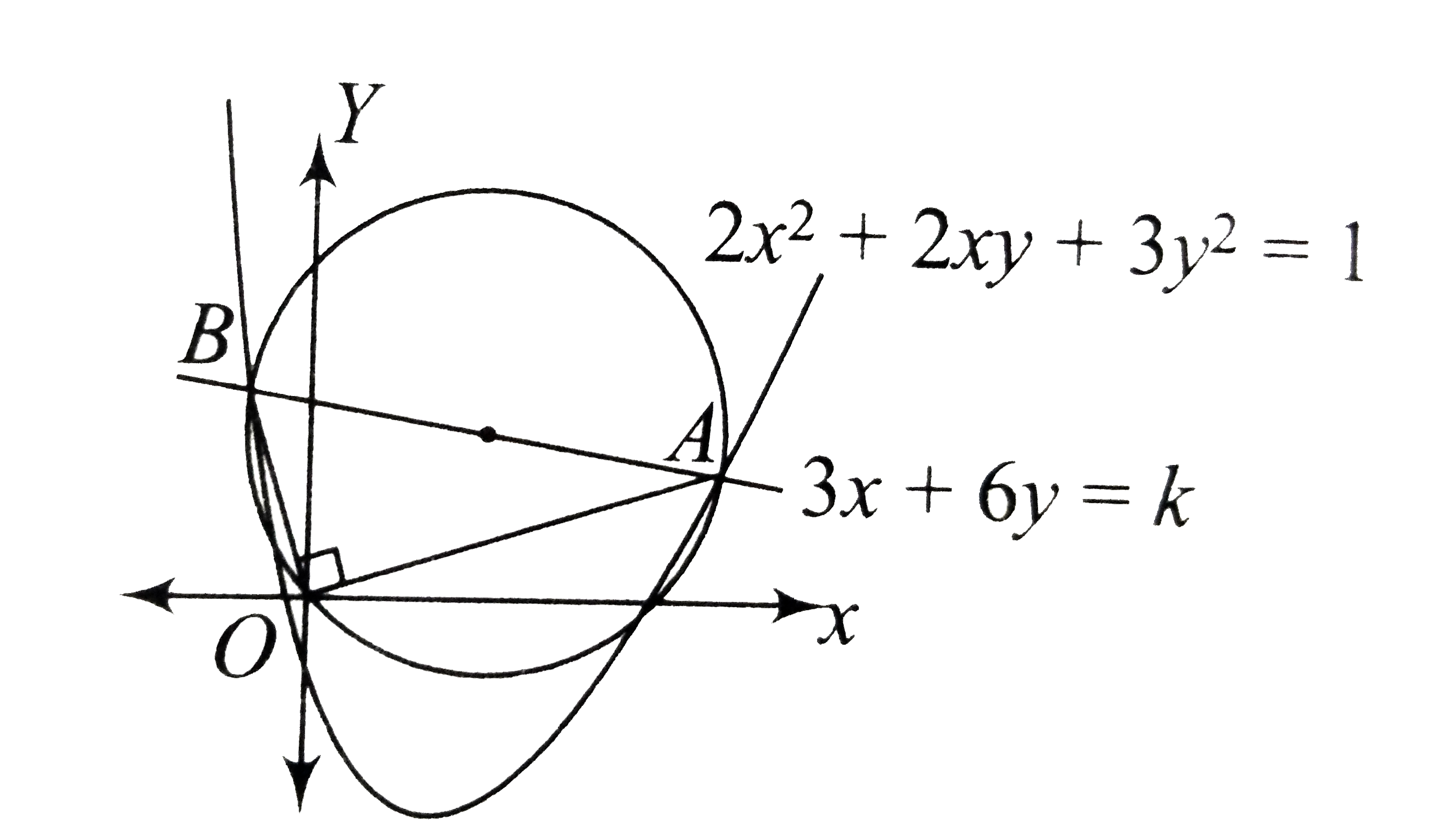
We have $\frac{3 x + 6 y}{k} = 1$ (1)
$2 x^{2} + 2 x y + 3 y^{2} - 1 = 0$ (2)
Now homogenising (2) with the help of (1), we get
$\Rightarrow 2 x^{2} + 2 x y + 3 y^{2} - {(\frac{3 x + 6 y}{k})}^{2} = 0$
$\Rightarrow k^{2} (2 x^{2} + 3 x + 3 y^{2}) - {(3 x + 6 y)}^{2} = 0$
Now, coefficient of $x^{2} +$ coefficient of $y^{2} = 0$
$\Rightarrow (2 k^{2} - 9) + (3 k^{2} - 36) = 0$
$\Rightarrow 5 k^{2} = 45 \Rightarrow k^{2} = 9 \Rightarrow k = 3$ or $- 3$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

CENGAGE-CIRCLES-Question Bank

Home
Ask Doubt
Profile