Let $f : [0, \infty) \to R$ be a continuous function such that $f (x) = 1 - 2 x + \int_{0}^{x} e^{x - t} f (t) d t for all x \in [0, \infty) .$ Then, which of the following statements(s) is (are)) TRUE?

A

The curve y=f(x) passes through the point (1,2)

B

The curve y=f(x) passes through the point (2,-1)

C

The area of the region ${(x, y) \in [0, 1] \times R : f (x) \leq y \leq \sqrt{1 - x^{2}}} is \frac{π - 2}{4}$

D

The area of the region ${(x, y) \in [0, 1] \times R : f (x) \leq y \leq \sqrt{1 - x^{2}}} is \frac{π - 1}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

$f (x) = 1 - 2 x + \overset{x}{\int_{0}} e^{x - 1} f (t) d t$
$\Rightarrow f (x) = 1 - 2 x + e^{x} \overset{x}{\int_{0}} e^{- t} f (t) d t ...(i)$
Differentiating w.r.t. x, we get
$f' (x) = - 2 + e^{x} e^{- x} f (x) + e^{x} \overset{x}{\int_{0}} e^{- t} f (t) d t ...(ii)$
Subtracting (i) from (ii), we get
$f' (x) - f (x) = - 2 + f (x) - 1 + 2 x$
$\Rightarrow f' (x) - 2 f (x) = 2 x - 3$
This is linear differential equation.
$I . F . = e^{\int - 2 d x} = e^{- 2 x}$
Therefore, solution is
$y \cdot e^{- 2 x} = \int (2 x - 3) e^{- 2 x} d x + c$
$\Rightarrow y \cdot e^{- 2 x} = (2 x - 3) \cdot \frac{e^{- 2 x}}{- 2} - \int 2 \times \frac{e^{- 2 x}}{- 2} d x + c$
$\Rightarrow y \cdot e^{- 2 x} = - \frac{(2 x - 3) e^{- 2 x}}{2} - \frac{e^{- 2 x}}{2} + c$
$\Rightarrow y \cdot e^{- 2 x} = (1 - x) e^{- 2 x} + c$
$\Rightarrow y = (1 - x) + c . e^{2 x} ...(iii)$
Putting x=0 in (i), we get f(0)=1.
So, from above equation, we have
$1 = 1 + c \Rightarrow c = 0$
Now, (iii) reduces to y=1-x, which passes through point (2,-1).
$Now, f (x) \leq y \leq \sqrt{1 - x^{2}}$
$\Rightarrow 1 - x \leq y \leq \sqrt{1 - x^{2}}$
$1 - x \leq y$ represents the region above the line $1 - x = y and y \leq \sqrt{1 - x^{2}}$ represents the region inside the semicircle (lying above x-axis) $x^{2} + y^{2} = 1 .$
So, common region is as the shaded one in the following figure :

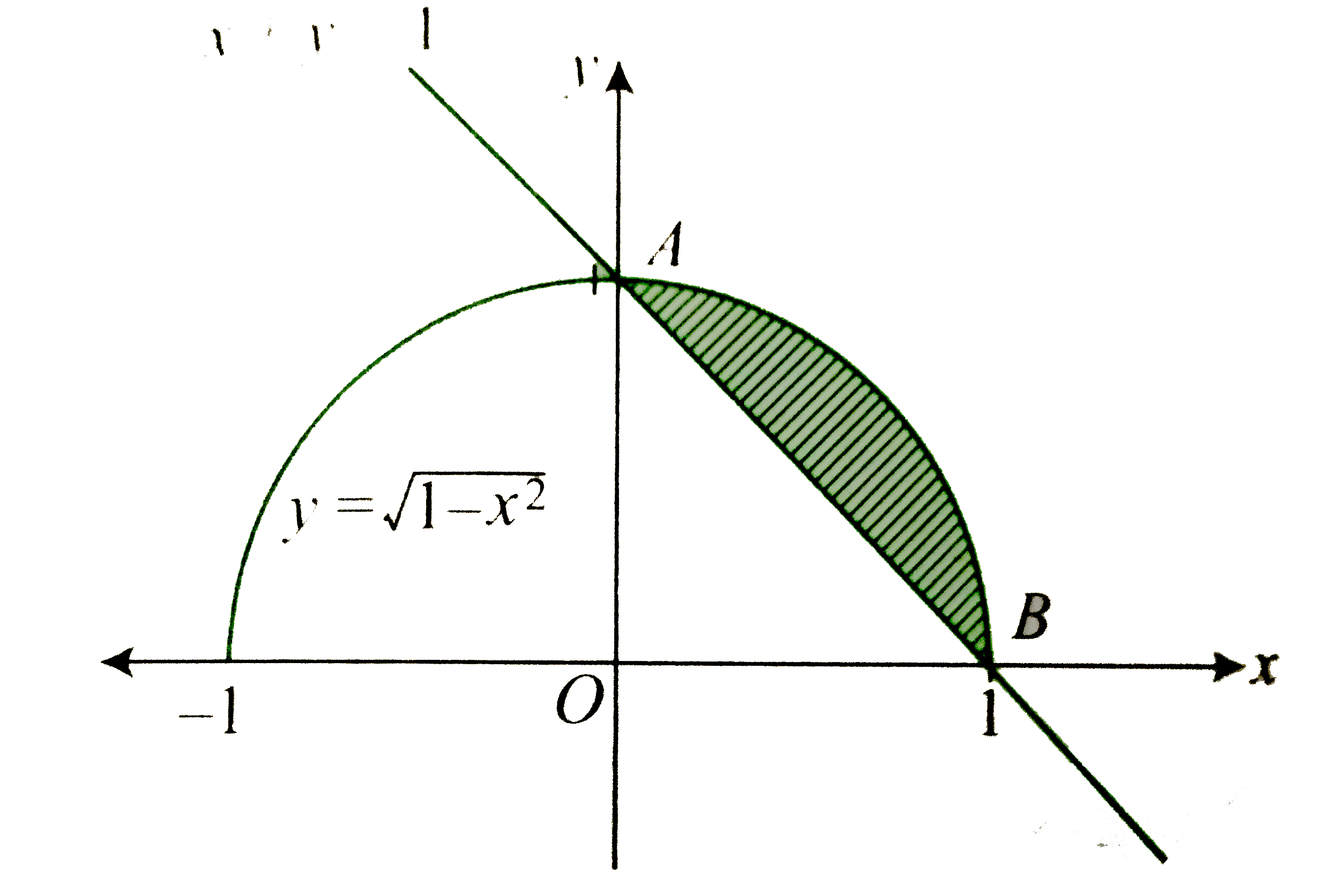
Area of the shaded region
=Area of quarter of the circle - Area of triangle OAB
$= \frac{1}{4} \times π {(1)}^{2} - \frac{1}{2} \times 1 \times 1 = \frac{π - 2}{4}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $f (x) = \int_{0}^{x} e^{t^{2}} (t - 2) (t - 3) d t$ for all $x \in (0, \infty)$ , then
Af has a local maximum at $x = 2$
Bf is decreasing on $(2, 3)$
Cthere exists some $c \in (0, \infty)$ such that $f (c) = 0$
Df has a local minimum at $x = 3$
Let $f : R \to R$ be a differentiable function such that $f (x) = x^{2} + \int_{0}^{x} e^{- t} f (x - t) d t$ .
$y = f (x)$ is
Ainjective but not surjective
Bsurjective but not injective
Cbijective
Dneither injective nor surjective
Let $f : R \to R$ be a differentiable function such that $f (x) = x^{2} + \int_{0}^{x} e^{- t} f (x - t) d t$ .
$f (x)$ increases for
A $x > 1$
B $x < - 2$
C $x > 2$
Dnone of these

CENGAGE-AREA-JEE Advanced Previous Year

Home
Ask Doubt
Profile