If 'a′(a>0) is the value of parameter for each of which the area of the figure bounded by the straight line y=a2−ax1+a4 and the parabola y=x2+2ax+3a21+a4 is the greatest, then the value of a4 is___
Video Solution
Text Solution
The correct Answer is:3
y=a2−ax1+a4 (1)
=x2+2ax+3a21+a4c (2)
Point of intersection of (1) and (2)
a2−ax1+a4=x2+2ax+3a21+a4
(x+a)(x+2a)=0
x=−a,−2a
Req. area =−a∫−2a[(a2−ax1+a4)−(x2+2ax+3a21+a4)]
∴ f(a)=a36(1+a4)
If f(a) is max, then f'(a)=0
⇒ 3+3a4−4a4=0
or a4=3
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Main Previous Year
10 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - JEE Advanced Previous Year
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)
4 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
If 'a′(a>0) is the value of parameter for each of which the area of the figure bounded by the straight line y=a2−ax1+a4 and the parabola y=x2+2ax+3a21+a4 is the greatest, then the value of a4 is___
View SolutionCompute the area of the figure bounded by the straight lines x=0, x=2 and the curves y=2x,y=2x−x2
View Solution
Knowledge Check
What is the area of the parabola x2=y bounded by the line y=1?
A13 sq. unitB23 sq. unitC43 sq. unitsD2 sq. unitsThe area of the region bounded by the lines y=2x+1y=3x+1 and x=4 is
A16 sq unitB1213 sq unitC1216 sq unitD8 sq unitFind the area of the figure bounded by the parabolas x=−2y2,x=1−3y2.
A83B63C43D23
Find the area of the figure bounded by the parabolas x=−2y2,x=1−3y2.
View SolutionFind the area of the region bounded by the parabola y2=2x and straight line x−y=4.
View SolutionCompute the area of the figure bounded by the parabolas x=−2y2,x=1−3y2
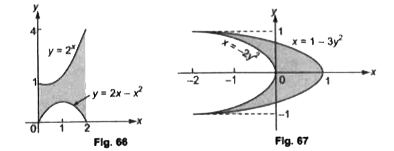
View SolutionFind the area of the gure bounded by the parabola y2=4xandx2=4y
View SolutionThe area of the reggion bounded by the lines y=2x+1,y=3x+1 and x=4 is
View Solution
