Find the area bounded by y=tan−1x,y=cot−1x,andy−aξs in the first quadrant.
Video Solution
Text Solution
The correct Answer is:log√2 sq. units
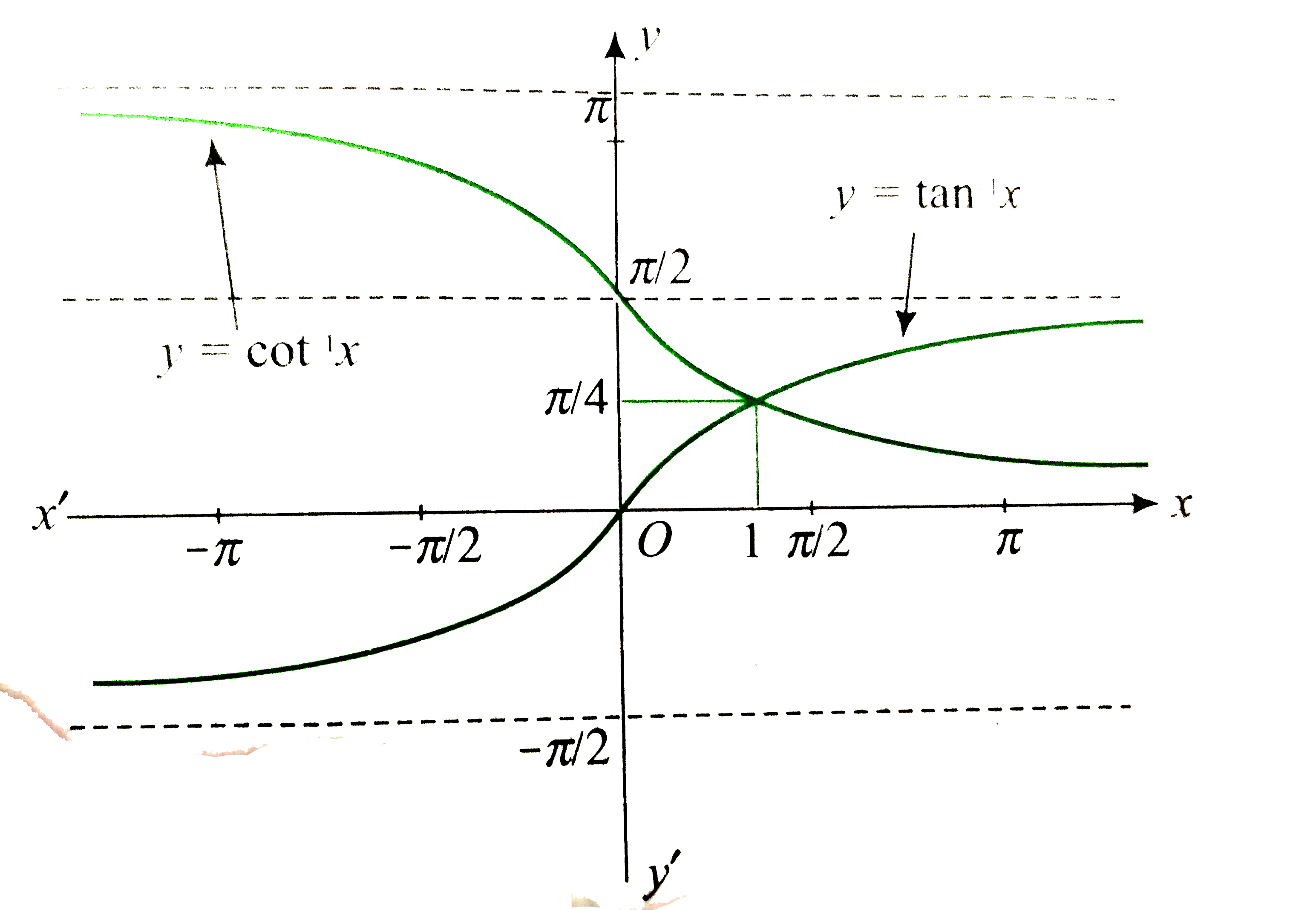
Intergrating along x-axis, we get
A=1∫0(cot−1x−tan−1x)dx=1∫0(π2−2tan−1x)dx
Intergrating a long y-axis, we get
A=2π/4∫0xdy=2.π/4∫0tanydy=[log(secy)]π/40
=log√2 sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.3
7 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Single)
40 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Question Bank
29 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
20 Videos
Similar Questions
Knowledge Check
Area bounded by y=tan−1x,y=cot−1x and y-axis is equal to
Aln √2 sq. unitBln 4 sq. unitCln 8 sq. unitDln 2 sq. unit
Find the area of the region bouonded by y2=4x,x=1,x=4 and x-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=8x,x=2,x=4 and the x-axis in the first quadrant.
View SolutionFind the area of the region bounded by x2=4y, y=2,y=4and the y-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=9x,x=2,x=4 and the x-axis in the first quadrant.
View SolutionFind the area bounded by the cirxle x2+y2=16 and the line y=x in the first quadrant .
View Solution
