Let f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.
f(x) is many-one but not an even function.
f(x) is a periodic function.
f(x) is a bounded function.
The graph of f(x) remains above the x-axis.
The correct Answer is:A, B, C, D
f(x)=sgn(cot−1x)+tan(π2[x])
sgn(cot−1x) is dedfined when cot−1x is defined, which is ∀x∈R.
tan(π2[x]) is defined when π2[x]≠(2n+1)2π, where n∈Z,
or[x]≠2n+1orx∈[2n+1,2n+2).
Hence, domain of f(x) is ∪n∈Z[2n,2n+1).
Also, cot−1x>0∀x∈R. Then
f(x)=1+tan(π2[x])=1
∴f(x)=1,x∈Df
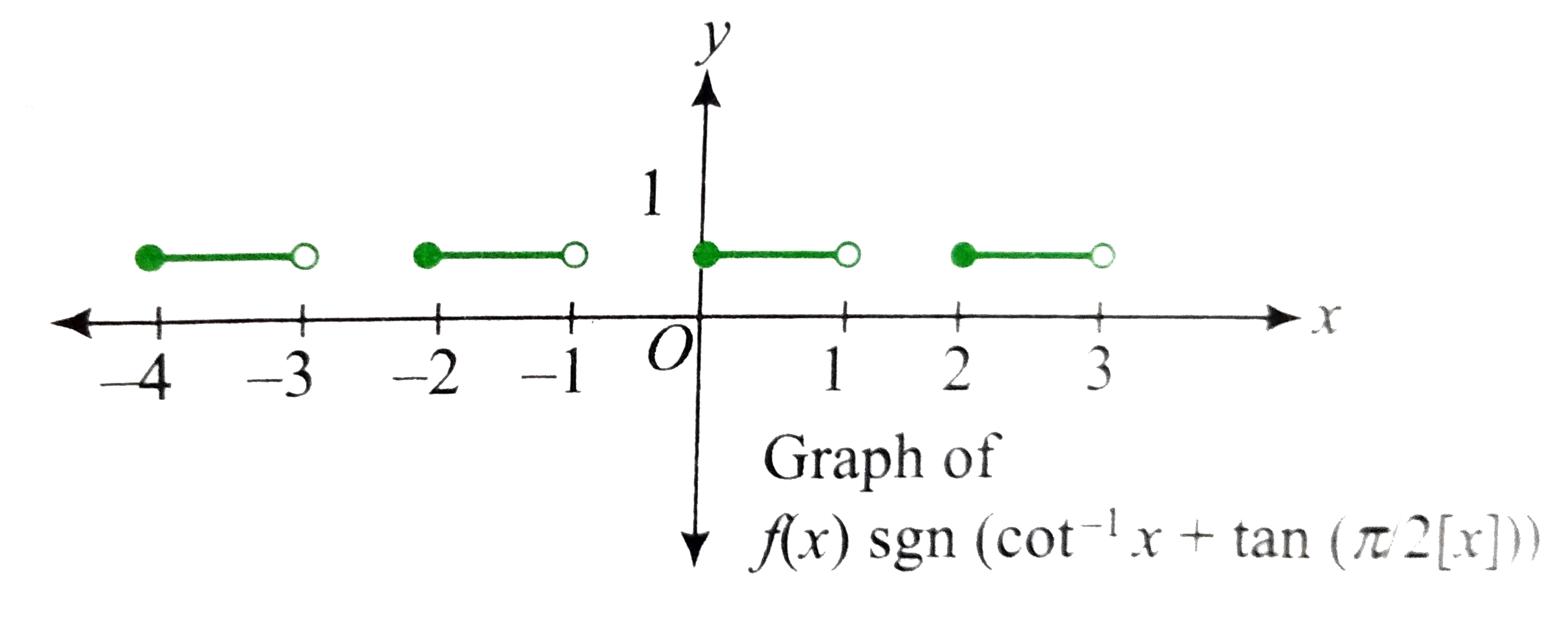
From the graph, f(x) si periodic with period 2.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)
125 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Let f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.
View Solutionf(x)=1√[x]−x, where [⋅] denotes the greatest integeral function less than or equals to x. Then, find the domain of f(x).
View Solution
Knowledge Check
For the function F (x) = [1[x]] , where [x] denotes the greatest integer less than or equal to x, which of the following statements are true?
Athe domain is (−∞,∞)Bthe range is {0} ∪ {-1} ∪ {1}Cthe domain is (−∞,0)∪[1,∞)Dthe range is {0} ∪ {1}The domain of the function f(x)=√x2−[x]2 , where [x] is the greatest integer less than or equal to x, is R (b) [0,+∞] (−∞,0) (d) none of these
ARB[0,∞)∪ZC(−∞,0]DR+Let f(x)=[x]cos(π[x+2]) where [ ] denotes the greatest integer function. Then, the domain of f is
AxεR,x not an integerBxε(−∞,−2)∪[−1,∞)CxεR,x≠−2Dxε(−∞,−1]
The function f(x)=x−[x]+cosx, where [x] = the greatest integer less than or equal to x is a
View SolutionLet f(x)=(−1)[x] where [.] denotes the greatest integer function), then
View SolutionLet f(x)=sin(tan−1x). Then [f(−√3)], where [⋅] denotes the greatest integer function, is
View SolutionThe function f(x)=tan|π[x−π]|1+[x]2, where [x] denotes the greatest integer less than or equal to x, is
View SolutionIf f(x)=esin(x−[x])cosπx, where [x] denotes the greatest integer function, then f(x) is
View Solution
