Question

Which of the following function is/are periodic?

Options

A. `f(x)={(1",",x " is rational"),(0",",x " is irrational"):}`
B. `f(x)={(x-[x]",",2n le x lt 2n+1),((1)/(2)",", 2n+1 le x lt 2n +2):}`
where [.] denotes the greatest integer function `n in Z`
C. `f(x)=(-1)^([(2x)/(pi)])`, where [.] denotes the greatest integer function
D. `f(x)=x-[x+3]+tan((pi x)/(2)),` where [.] denotes the greatest integer function, and a is a rational number

Answer

A::B::C::D

Explanation

`f(x)={(1",",x " is rational"),(0",",x " is irrational"):}`
`or f(x+k)={(1",",x+k " is rational"),(0",",x+k " is irrational"):}`, where k is any rational number
`={(1",",x " is rational"),(0",",x " is irrational"):}`
`=f(x)`
Therefore, `f(x)` is periodic function, but its fundamental period cannot be determined. Thus,
`f(x)={(x-[x]",",2n le x lt 2n+1),(1//2",", 2n+1 le x lt 2n +2):}`
Draw the graph from which it can be verified that period is 2.

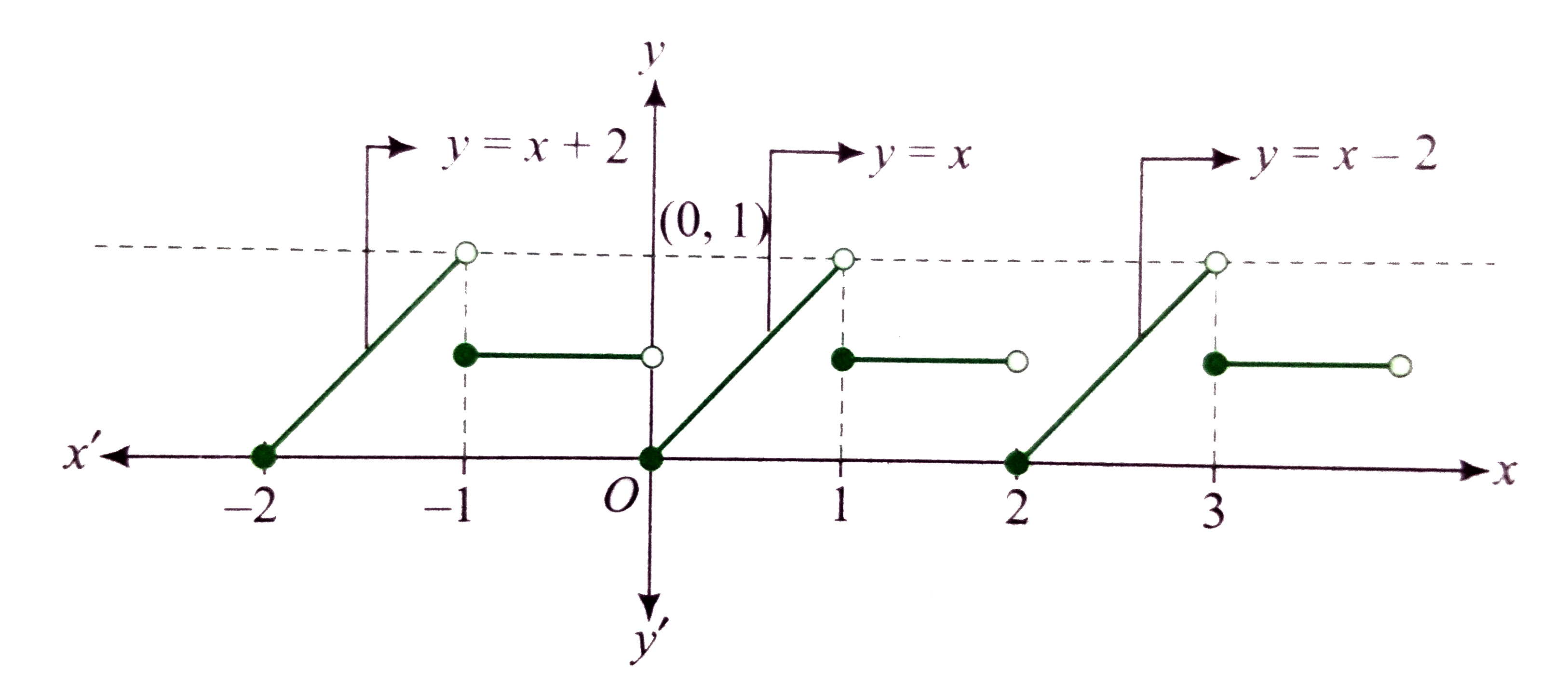
`f(x)=(-1)^([(2x)/(pi)])`
`or f(x+pi)=(-1)^([(2(pi+x))/(pi)])=(-1)^([(2x)/(pi)]+2)=(-1)^([(2x)/(pi)])`
Hence, the period is `pi`.
`f(x)=x-[x+3]+tan((pix)/(2))={x}-3+tan((pi x)/(2))`
{x} is periodic with period `1, tan((pi x)/(2))x` is period with period 2.
Now, the LCM of 1 and 2 is 2. Hence, the period of `f(x) ` is 2.