Solve |x−1|+|x−2|≥4
Video Solution
Text Solution
Let f(x)=|x−1|+|x−2|
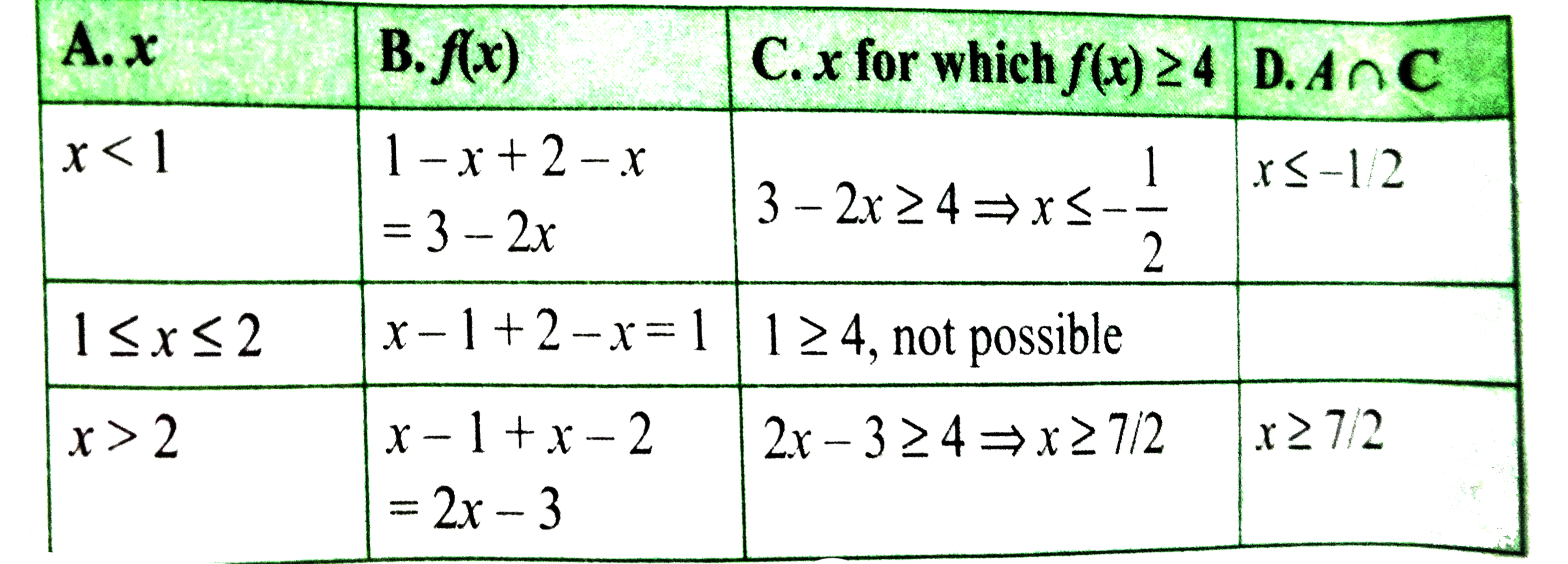
Hence, solutions is x∈(−∞,−1/2]∪[7/2,∞).
Alternative Method:
Consider |x−1|+|x−2|<4
Now, |(x−1)+(x−2)|≤|x−1|+|x−2|
∴|(x−1)|+(x−2)∣<4
⇒|2x−3|<4
⇒−4<2x−3<4
⇒−1<2x<7
⇒−1/2<x<7/2
Therefore, for |x−1|+|x−2|≥4, we have
x∈(−∞,−1/2]∪[7/2,∞).
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise 1.1
Explore 15 Videos
- RELATIONS AND FUNCTIONSBook:CENGAGEChapter:RELATIONS AND FUNCTIONSExercise:Exercise 1.2
Explore 5 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBook:CENGAGEChapter:Quadratic Equations, Inequalities, Modulus and LogarithmsExercise:Question Bank
Explore 31 Videos
- SCALER TRIPLE PRODUCTS Book:CENGAGEChapter:SCALER TRIPLE PRODUCTS Exercise:DPP 2.3
Explore 11 Videos
Similar Questions
Knowledge Check
solve: |x−2|+|x−4|≥8
Ax∈(−∞,−1]∪[7,∞)Bx∈(−∞,3]∪[7,∞)Cx∈(−7,−1]∪[7,∞)Dx∈[7,∞)
Solve ||x−1|−5|≥2.
View SolutionSolve the following systems of inequalities for all x∈R
Solve (|x|−1)(|x|−2)≥0,x∈R,x is not equal to ±2
View SolutionSolve |x−3|≥4
View SolutionSolve |x−3|≥2
View SolutionSolve : |x−1|+|x−2|≥3
View SolutionSolve: −1|x|−2≥1.
View SolutionSolve:
|x|−1|x|−2≥0,x∈R−{−2,2}
View Solution