The intensity at the maximum in a Young's double slit experiment is $I_{0^{.}}^{.}$ Distance between two slits is $d = 5 λ,$ where $λ$ is the wavelength of light used in the experment. What will be that intensity in front of one of the slit on the screen placed at a distance at a distance D=10 d ?

A

$\frac{I_{0}}{4}$

B

$\frac{3}{4} I_{0}$

C

$\frac{I_{0}}{2}$

D

$I_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Consider the given diagram, where $S_{1} and S_{2}$ are two slits. The path difference for point P is given by :

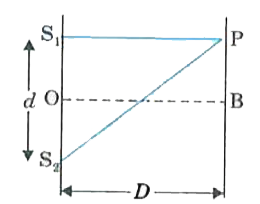
$Δ x = S_{2} P - S_{1} P = \sqrt{D^{2} + d^{2}} - D$
$= D (1 + \frac{d^{2}}{2 D^{2}}) - D = \frac{d^{2}}{2 D}$
Given that, $D = 10 d, Δ x = \frac{d^{2}}{2 (10 d)} = \frac{d}{20}$
Now, $d = 5 λ Δ x = \frac{5 λ}{20} = \frac{λ}{4}$
Therefore, the phase difference is given by :
$Δ ϕ = \frac{2 π}{λ} \times \frac{λ}{4} = \frac{π}{2}$
Thus, the intensity is given by :
$I = I_{0} \frac{{cos}^{2} ϕ}{2} = I_{0} \frac{{cos}^{2} (π)}{4} = \frac{I_{0}}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The intensity at the maximum in a Young's double slit experiment is $I_{0^{.}}^{.}$ Distance between two slits is $d = 5 λ,$ where $λ$ is the wavelength of light used in the expermient. What will be that intensity infront of one of the slite on the screen placed at a distance at a distance D=10 d ?
A $\frac{I o}{2}$
B $\frac{I o}{4}$
C $\frac{I o}{8}$
D $\frac{I o}{16}$
Question 2 - Select One
The intensity at the maximum in a Young's double slit experiment is $I_{0^{.}}^{.}$ Distance between two slits is $d = 5 λ,$ where $λ$ is the wavelength of light used in the experment. What will be that intensity in front of one of the slit on the screen placed at a distance at a distance D=10 d ?
A $I_{0}$
B $\frac{I_{0}}{4}$
C $\frac{3}{4} I_{0}$
D $\frac{I_{0}}{2}$
Question 3 - Select One
The maximum intensity in young's double-slit experiment is $I_{0}$ . Distance between the slit is $d = 5 λ$ , where $λ$ is the wavelength of monochromatic light used in the experiment. What will be the intensity of light in front of one of the slits on a screen at a distance $D = 10 d$ ?
A $\frac{I_{0}}{2}$
B $\frac{3}{4} I_{0}$
C $I_{0}$
D $\frac{I_{0}}{4}$

MODERN PUBLICATION-WAVE OPTICAL-OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS) -AIPMT/NEET & OTHER STATE BOARDS FOR MEDICAL ENTRANCE

Home
Ask Doubt
Profile