Fig. shows an experimental set up simillar to Young's double slit experiment to observe interference of light. Here . Write down the conditions of (i) Contstructive interference
(ii) Destructive interference at any point in terms of path diff. . Does the central fringe observed in the above set up lie above or below ? Give reason.
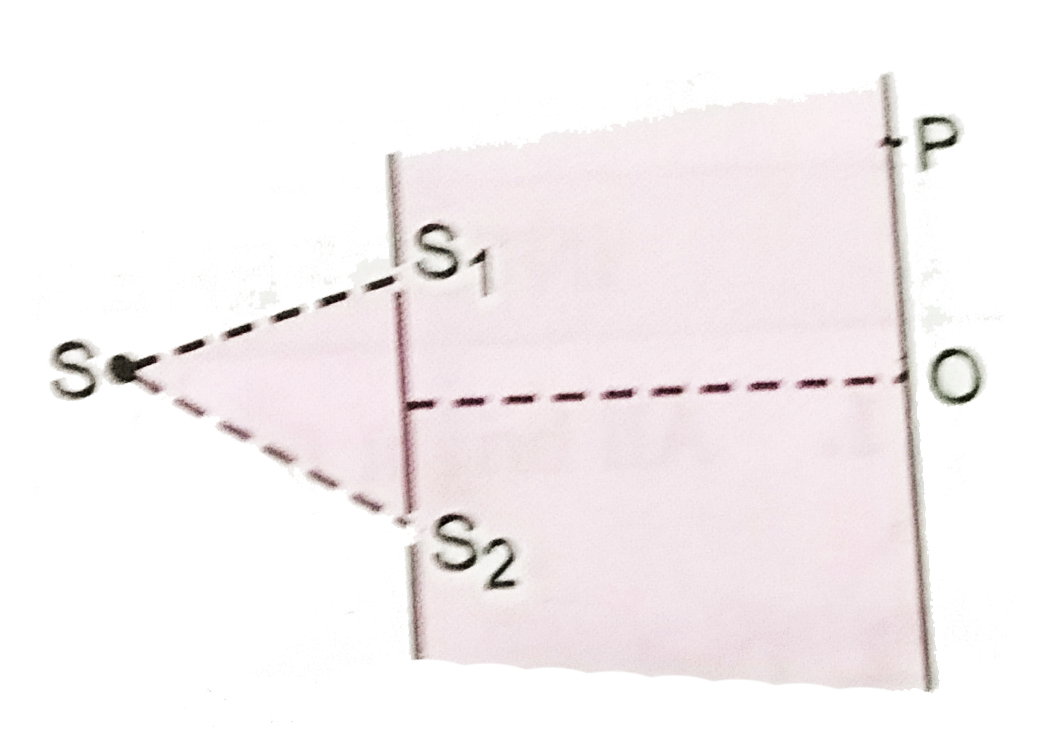
Initial path difference between sources
Let , the path difference between disturbances
from
Total path difference =
For constructive interference,
For destructive interference,
(b) For central fringe putting n = 0 in (1) we get
The negative sign indicates that the central fringe lies below the central point.
Topper's Solved these Questions
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:Revision Exercises (Long Answer Questions)
Explore 9 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:Revision Exercises (Numerical Problems)
Explore 31 Videos
- WAVE OPTICALBook:MODERN PUBLICATIONChapter:WAVE OPTICALExercise:Revision Exercises (Fill in the Blanks)
Explore 10 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
The figure shows a modified Young’s double slit experimental set-up. Here SS2−SS1=λ/4.
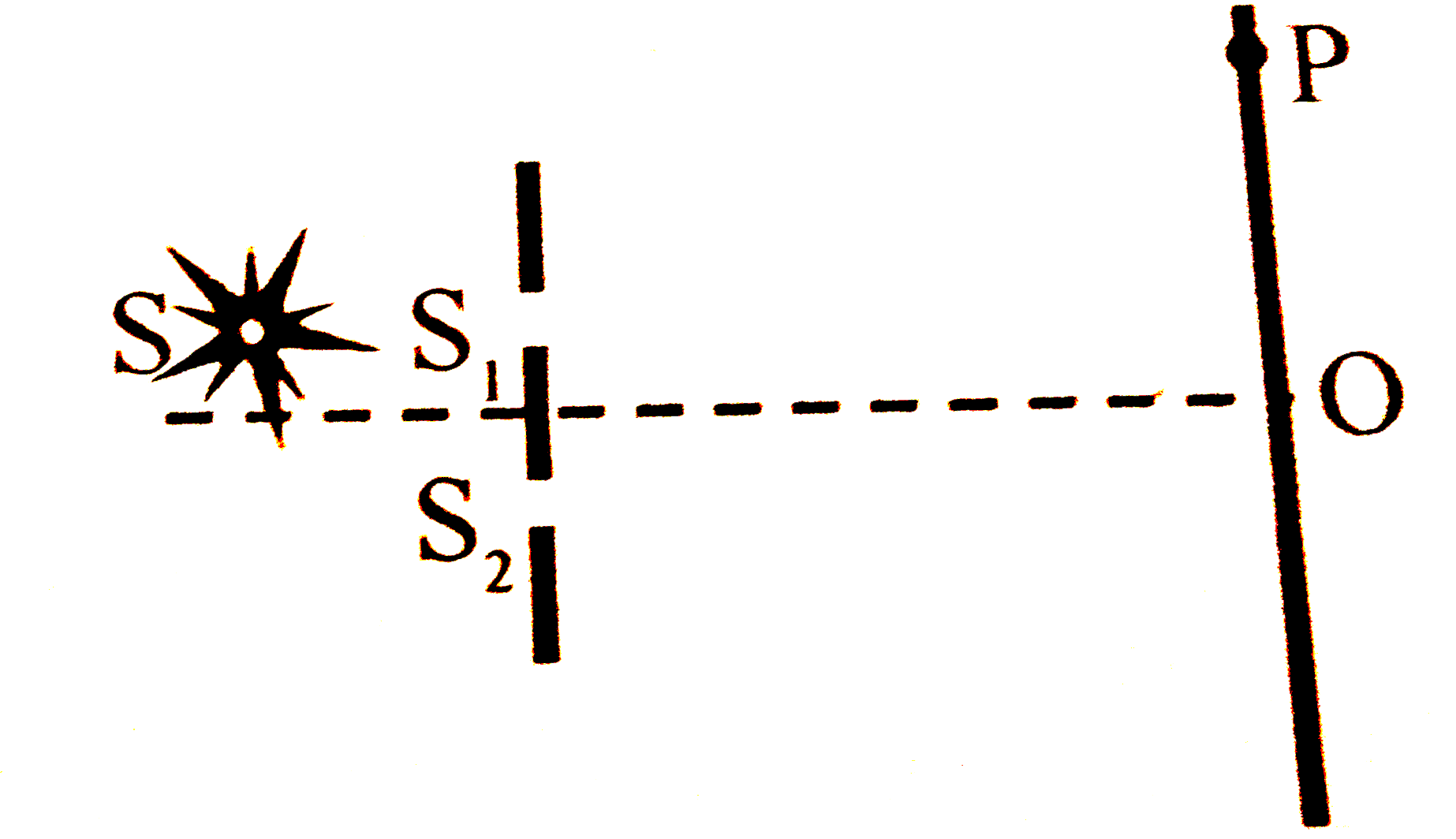
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
View SolutionThe figure shows a modified Young's double slit experimental set-up.
Here SS2−SS1=λ/4.
(a) Write the condition for constructive interference.
(b) Obtain an expression for the fringe width.
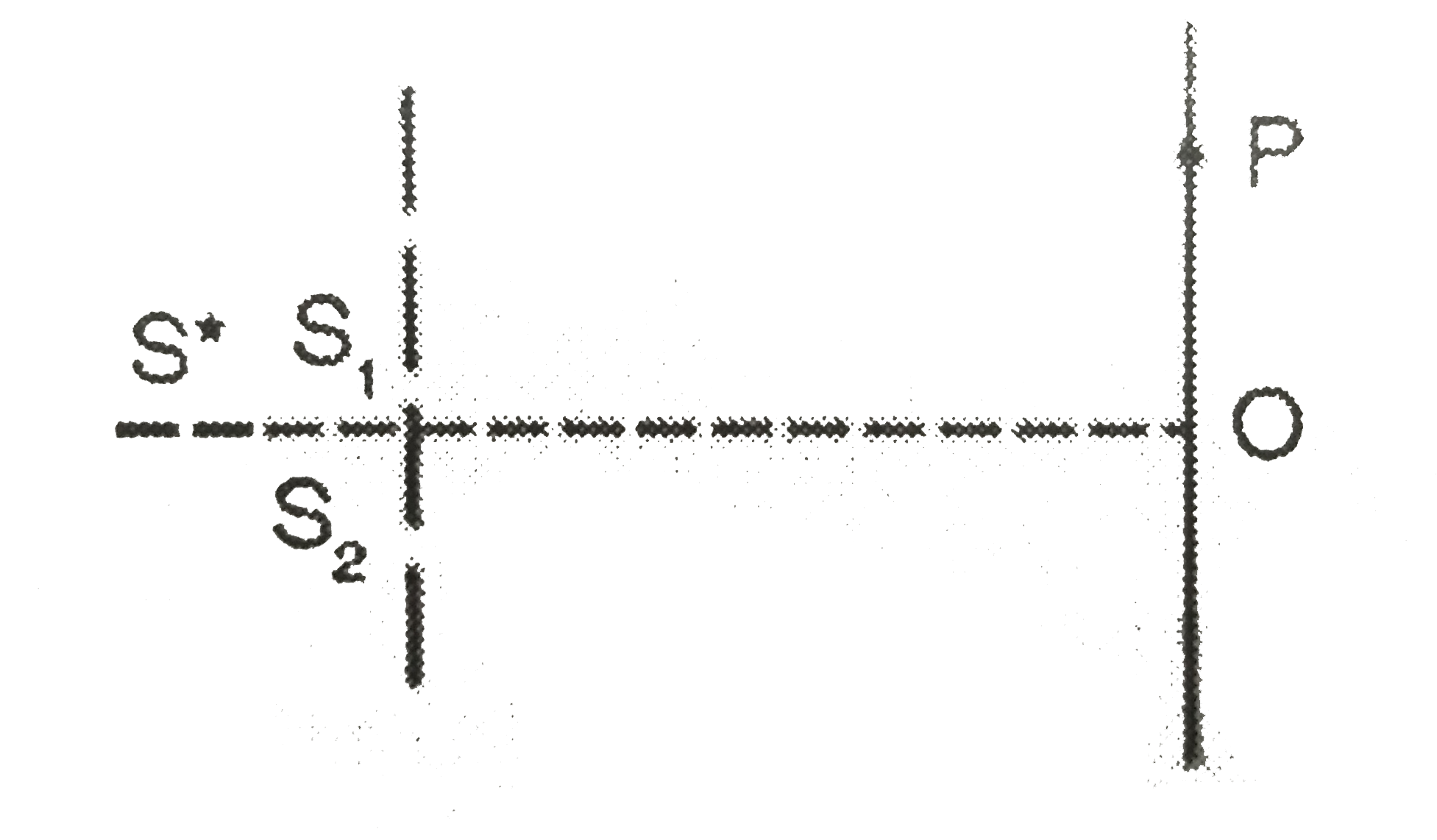
View Solution
Knowledge Check
At two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
A2:1B√2:1C4:1D3:2At two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
A3:2B2:1C√2:1D4:1Let S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
Aλ/θBλθC2λ/θDλ/2θ
In a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.
View SolutionIn Young's double-slit experiment, the point source is placed slightly off the central axis shown in Fig. 2.45.
a. Find the nature and order of the interference at point P.
b. Find the nature and order of the interference at point. O.

View Solution(a) In Young's double-slit experiment, derive the condition for
(i) constructive interference and (ii) destructive interference ata point on the screen.
(b) A beam of light consisting of two wavelenths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double-slit experiment on a screen placed 1.4m away. if the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
View Solution(a) In Young's double slit experiment, derive the condition for (i) constructive interference and (ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference frings in a Young's double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000Å, coming from the coherent sources S1 and S2. At certain point P on the screen third dark fringe is formed. Then the path difference S1P−S2P in microns is
View Solution

