If Z=√R2+(XC−XL)2 then give the phase relationship of current and voltage.
To determine the phase relationship between current and voltage in an AC circuit given the impedance Z=√R2+(XC−XL)2, we can follow these steps:
Step 1: Understand the Components
- Identify the components involved:
- R is the resistance.
- XL is the inductive reactance.
- XC is the capacitive reactance.
Step 2: Draw the Phase Diagram
- Draw a phase diagram where:
- The horizontal axis represents the resistance R.
- The vertical axis represents the net reactance (XL−XC).
Step 3: Determine the Voltage and Current Relationships
- The voltage across the inductor VL leads the current I by 90∘.
- The voltage across the capacitor VC lags the current I by 90∘.
- Therefore, the net voltage Vnet can be represented as VL−VC.
Step 4: Calculate the Impedance
- The impedance Z can be expressed as:
Z=√R2+(XL−XC)2
Step 5: Find the Phase Angle ϕ
- The phase angle ϕ between the current and voltage can be calculated using:
cosϕ=RZ
- Substituting Z:
cosϕ=R√R2+(XL−XC)2
Step 6: Use the Tangent Function
- Alternatively, you can express the tangent of the phase angle:
tanϕ=XL−XCR
- Therefore, the phase angle ϕ can also be expressed as:
ϕ=tan−1(XL−XCR)
Conclusion
- The phase relationship between current and voltage in the circuit can be summarized by the phase angle ϕ, which indicates whether the circuit is capacitive or inductive based on the values of XL and XC.
- Identify the components involved:
- R is the resistance.
- XL is the inductive reactance.
- XC is the capacitive reactance.
- Draw a phase diagram where:
- The horizontal axis represents the resistance R.
- The vertical axis represents the net reactance (XL−XC).
Step 3: Determine the Voltage and Current Relationships
- The voltage across the inductor VL leads the current I by 90∘.
- The voltage across the capacitor VC lags the current I by 90∘.
- Therefore, the net voltage Vnet can be represented as VL−VC.
- The impedance Z can be expressed as:
Z=√R2+(XL−XC)2
- The phase angle ϕ between the current and voltage can be calculated using:
cosϕ=RZ
- Substituting Z:
cosϕ=R√R2+(XL−XC)2
- Alternatively, you can express the tangent of the phase angle:
tanϕ=XL−XCR
- Therefore, the phase angle ϕ can also be expressed as:
ϕ=tan−1(XL−XCR)
- The phase relationship between current and voltage in the circuit can be summarized by the phase angle ϕ, which indicates whether the circuit is capacitive or inductive based on the values of XL and XC.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Revision Exercises ( Additional Questions )
Explore 10 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Revision Exercises (Fill in the Blanks )
Explore 10 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
Explore 7 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
A series circuit consisting of a capacitor XC=80Ω and a coil with active resistance R=300Ω and inductance XL=40ω is connected to a source of alternating voltage with amplitude V0=200V Find
(a) the current amplitude in the circuit
(b) the phase difference between the current and voltage
(c) the amplitudes of voltage across the capacitor and the coli .
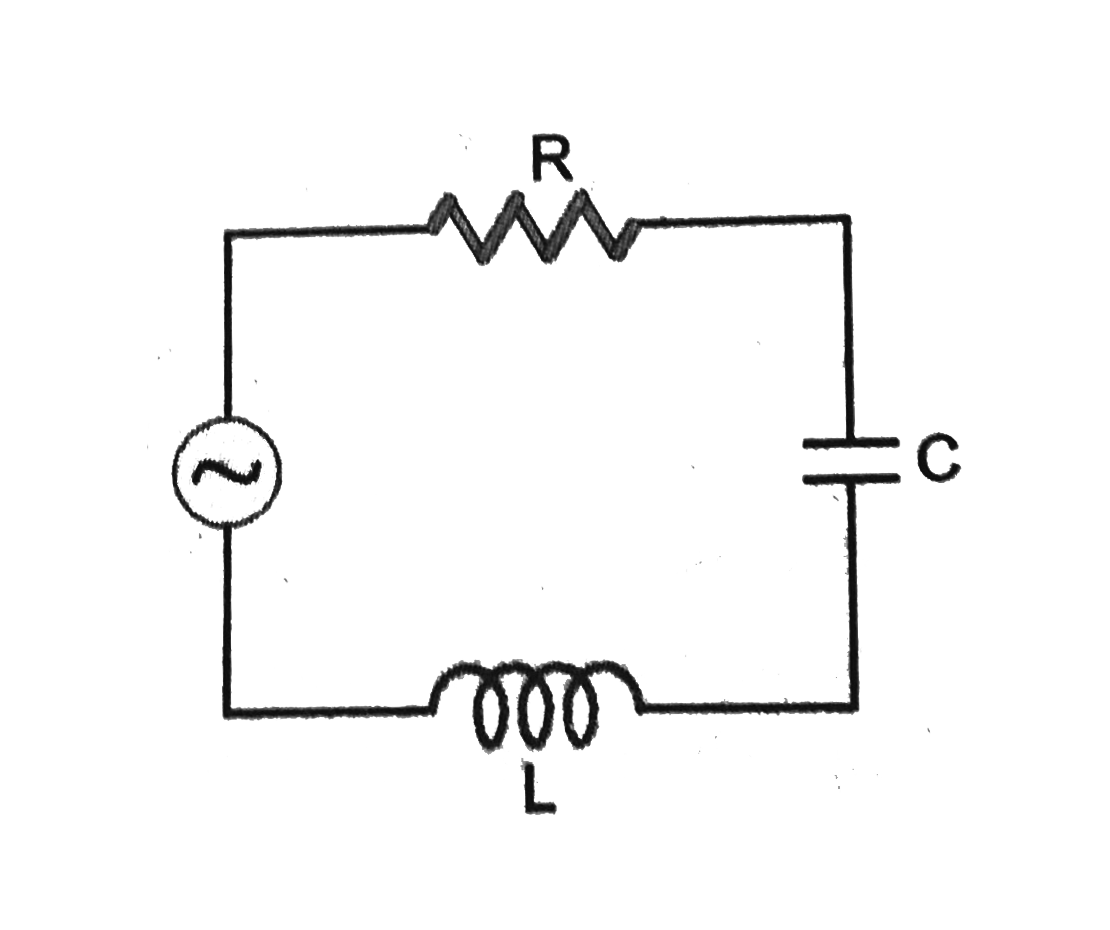
View SolutionFig. show a series LCR circuit with L=0.1Hl,XC=14Ω and R=12Ω connected to a 50 Hz, 200 V source. Calculate
(i) current in the circuit and
(ii) phase angle between current and voltage.
Take π=3
View Solution
Knowledge Check
In an AC circuit XC=XL. The phase differe3nce between the current and voltage will be
A0BπCπ/2Dπ/4In a series LCR circuit, resistance R = 10 Ω and the impedance z = 20 Ω . The phase difference between the current and voltage is
Aπ6Bπ4Cπ3Dπ2In a series LCR circuit, resistance R=10Ω and the impedence Z=20Ω the phase difference between the current and the voltage is
A30∘B45∘C60∘D90∘
In L-C-R series circuit suppose ωr is resonance frequency, then match the following table,
Table-1Table-2(A)If ω>ωr(P)Current will lead the voltage(B)If ω=ωr(Q)Voltage will lead the current(C)If ω=2ωr(R)XL=2XC(D)If ω<ωr(S)Current and voltage are in phase(T)None
View SolutionWhat is the phase relationship between voltage and current in an AC circuit containing only resistance ?
View SolutionA coil with inductive reactance XL=30Ω and impedance Z=50Ω is connected to the mains with effective voltage value V=100V Find the phase difference between the current and voltage as well as the heat power generated in the coil .
View SolutionConsider the salt KxHy(C2O4)z.2H2O. The relationship between x,y and z is
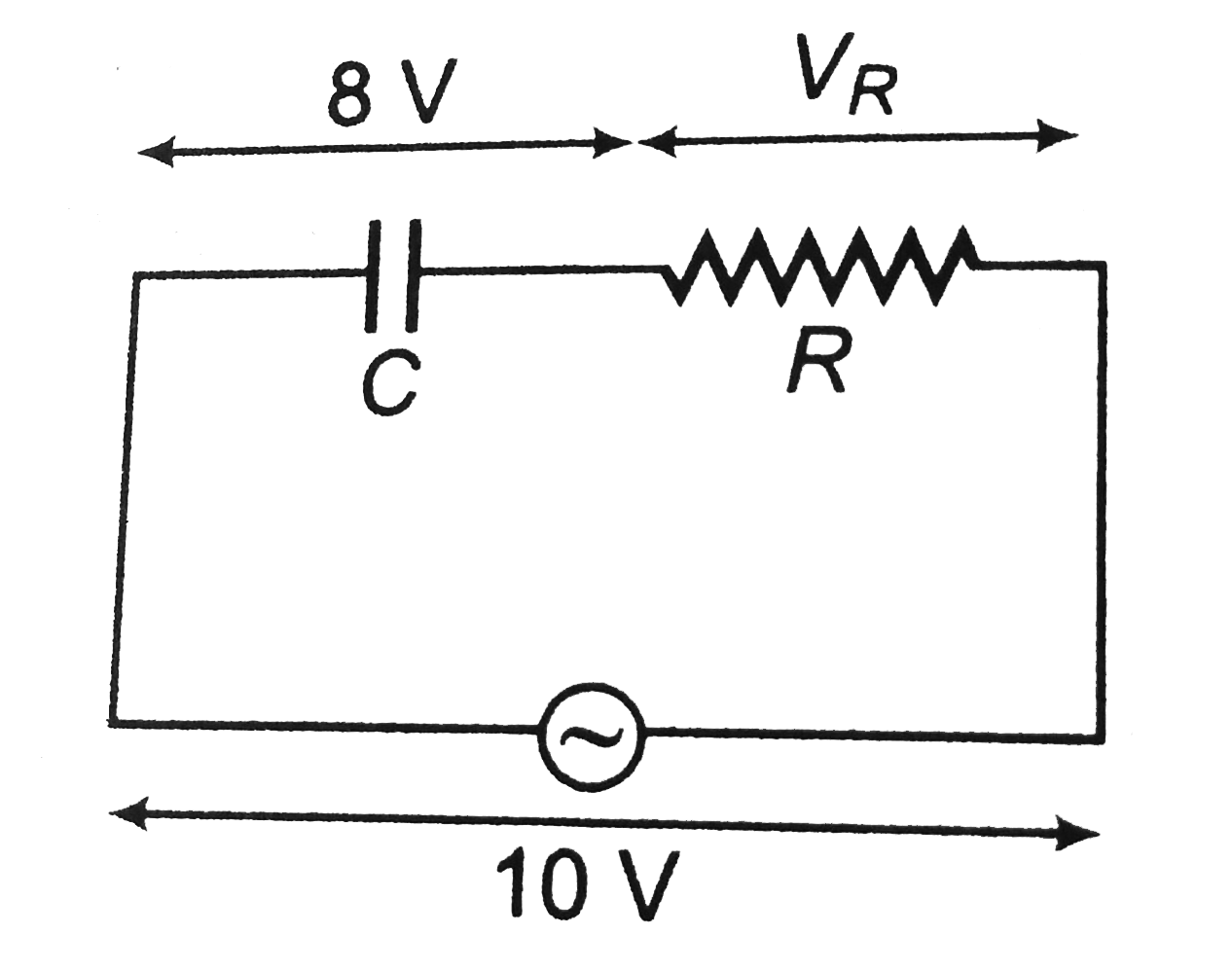
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
 .
.
View Solution