How the reactance of an inductor depends on frequency ?
To understand how the reactance of an inductor depends on frequency, we can follow these steps:
Step 1: Understand the Concept of Reactance
Reactance (X_L) is the opposition that an inductor offers to the flow of alternating current (AC). It is frequency-dependent and is given by the formula:
XL=ωL
where:
- XL = inductive reactance
- ω = angular frequency (in radians per second)
- L = inductance (in henries)
Step 2: Relate Angular Frequency to Frequency
Angular frequency (ω) is related to the frequency (f) of the AC supply by the formula:
ω=2πf
This means that as the frequency increases, the angular frequency also increases.
Step 3: Substitute Angular Frequency in the Reactance Formula
Substituting the expression for angular frequency into the reactance formula gives:
XL=(2πf)L
This shows that the inductive reactance is directly proportional to the frequency.
Step 4: Analyze the Relationship
From the equation XL=2πfL, we can conclude that:
- As the frequency (f) increases, the inductive reactance (X_L) also increases.
- This indicates that at higher frequencies, the inductor will oppose the current more strongly.
Step 5: Graphical Representation
If we were to plot a graph of inductive reactance (X_L) against frequency (f), we would see a straight line passing through the origin, indicating a linear relationship. The slope of this line would be 2πL.
Conclusion
In summary, the reactance of an inductor increases linearly with the frequency of the alternating current. This means that as the frequency of the AC supply increases, the opposition offered by the inductor to the current flow also increases.
---
Reactance (X_L) is the opposition that an inductor offers to the flow of alternating current (AC). It is frequency-dependent and is given by the formula:
XL=ωL
where:
- XL = inductive reactance
- ω = angular frequency (in radians per second)
- L = inductance (in henries)
Angular frequency (ω) is related to the frequency (f) of the AC supply by the formula:
ω=2πf
This means that as the frequency increases, the angular frequency also increases.
Substituting the expression for angular frequency into the reactance formula gives:
XL=(2πf)L
This shows that the inductive reactance is directly proportional to the frequency.
From the equation XL=2πfL, we can conclude that:
- As the frequency (f) increases, the inductive reactance (X_L) also increases.
- This indicates that at higher frequencies, the inductor will oppose the current more strongly.
If we were to plot a graph of inductive reactance (X_L) against frequency (f), we would see a straight line passing through the origin, indicating a linear relationship. The slope of this line would be 2πL.
In summary, the reactance of an inductor increases linearly with the frequency of the alternating current. This means that as the frequency of the AC supply increases, the opposition offered by the inductor to the current flow also increases.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Revision Exercises ( Additional Questions )
Explore 10 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:Revision Exercises (Fill in the Blanks )
Explore 10 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:HIGHER ORDER THINKING SKILLS & ADVANCED LEVEL
Explore 7 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
Calculate the capacitance of a capacitro connected across an alternating power supply with the reactance equal to the reactance of an inductor coil of 1H. The frequency of power supply is 200 Hz.
View Solution(a) What is the reactance of a 2.00H inductor at a frequency of 50.0Hz?
(b) What is the inductance of an inductor whose reactance is 2.00Ω at 50.0Hz?
(c) What is the reactance of a 2.00μF capacitor at a frequency of 50.0Hz?
(d) What is the capacitance of a capacitor whose reactance is 2.00Ω at 50.0Hz?
View Solution
Knowledge Check
A : An inductor and a capacitor are called low pass filter and high pass filter respectively.
R : Reactance of an inductor is low for low frequency signals and that of a capacitor is high for high frequency signals.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion, then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion, then mark (2)CIf Assertion is true statement but Reason is false, then mark (3)DIf both Assertion and Reason are false statement, then mark (4)
Sketch a graph showing the variation of reactance of an inductor with frequency of the applied voltage
View SolutionHow inductive reactance depends on the frequency of AC ?
View SolutionHow capacitive reactance depends on the frequency of AC ?
View SolutionThe figure shows the graphical variation of the reactance of a capacitor with frequency of ac source. (a) find the capacitance of the capacitor (b)an ideal inductor has the same reactance at 100 Hz frequency as the capacitor has the same frequency find the value of the inductor. (c) draw the graph showing the variation of the reactance of this inductor with frequency

View SolutionHow does the pitch of a sound depend on frequency?
View SolutionThe figure shows the graphical variation of the rectance of a capacitor with frequency of acsource.
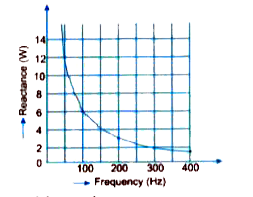
(a) Find the capacitance of the capacitor.
(b) An ideal inductor has the same reactance at 100 Hz frequency as the capacitor has at the same frequency. Find the value of inductance of the inductor.
(c ) Draw the graph showing the variation of the rectance of this inductor with frequency.
View SolutionExplain why the reactance offered by an inductor increases with increasing frequency of an alternating voltage.
View Solution

