A 0.05 H inductor is connected to a fully charged 80 μF capacitor. The maximum current in the inductor is found to be 2 A. Calculate the voltage across capacitor while it was getting charged.
The correct Answer is:50A
To solve the problem, we need to calculate the voltage across the capacitor while it was getting charged. We will use the energy conservation principle, where the energy stored in the capacitor is equal to the energy stored in the inductor at maximum current.
1. Identify the given values:
- Inductance (L) = 0.05 H
- Capacitance (C) = 80 µF = 80 × 10^(-6) F
- Maximum current (I) = 2 A
2. Write the formula for energy stored in the capacitor:
The energy (E) stored in the capacitor is given by the formula:
Ecapacitor=12CV2
where V is the voltage across the capacitor.
3. Write the formula for energy stored in the inductor:
The energy stored in the inductor is given by:
Einductor=12LI2
4. Set the energies equal to each other:
Since the energy in the capacitor is converted to energy in the inductor, we have:
12CV2=12LI2
5. Cancel the 12 from both sides:
CV2=LI2
6. Rearrange the equation to solve for V:
V2=LI2C
V=√LI2C
7. Substitute the known values into the equation:
V=√0.05H⋅(2A)280×10−6F
8. Calculate the values:
V=√0.05⋅480×10−6
V=√0.280×10−6
V=√2500=50V
9. Conclusion:
The voltage across the capacitor while it was getting charged is 50 volts.
- Inductance (L) = 0.05 H
- Capacitance (C) = 80 µF = 80 × 10^(-6) F
- Maximum current (I) = 2 A
The energy (E) stored in the capacitor is given by the formula:
Ecapacitor=12CV2
where V is the voltage across the capacitor.
The energy stored in the inductor is given by:
Einductor=12LI2
Since the energy in the capacitor is converted to energy in the inductor, we have:
12CV2=12LI2
CV2=LI2
V2=LI2C
V=√LI2C
V=√0.05H⋅(2A)280×10−6F
V=√0.05⋅480×10−6
V=√0.280×10−6
V=√2500=50V
The voltage across the capacitor while it was getting charged is 50 volts.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CONCEPTUAL QUESTIONS
Explore 25 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:TOUGH & TRICKY PROBLEMS
Explore 12 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
An L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4×10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View SolutionAn L−C circuit consists of an inductor coil withh L=50.0mH and 20.0μF capacitor. There is negligible resistance in the circuit. The circuit is driven by a voltage source with V=V0cosωt. If V0=5.00mV and the frequency is twice the resonance frequency, determine.
a. the maximum charge on the capacitor.
b. the maximum current in the circuit.
c. the phase relationship between the voltages across the inductor, the capacitor and the sourse.
View Solution
Knowledge Check
A non-resistive inductor is connected across a fully charged capacitor and the L-C circuit is set oscillating at its natural frequency. What is the value of the current when the charge on the capacitor has the maximum value of 100μC?
AZeroBInfinityC10μAD100μAAn inductor L is allowed to discharge through capacitor C. The emf induced across the inductance when the capacitor is fully charged is
AmaximumBminimumCzeroDinfiniteEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.
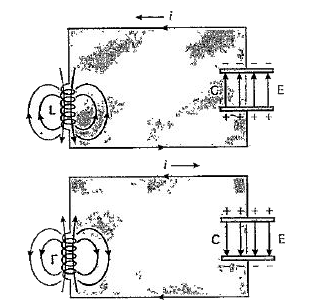
A capacitor of 25μF and inductor of 0.6 H are in an LC circuit. When the charge on capacitor is3×10−5C, what is the rate of change of current:A2 A/sB3 A/sC4 A/sD6 A/s
A charged 8mF capacitor having charge 5mC is connected to a 5mH inductor. What is :
(iii) the maximum current in the inductor?
View SolutionEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.

We cannot use LC oscillator:to, produce:
View SolutionEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.

If we increase the value or L four times in LC oscillator, the frequency of oscillation is:
View SolutionEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.

For LC oscillator, the frequency of oscillator is:
View SolutionIn the given circuit, if initial charge on the capacitor is 100μC, then the maximum current is (Initially, the inductor is fully deenergized)
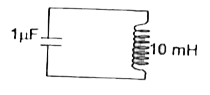
View Solution

