In a series LCR circuit with value of R = 15 Ω,L=5H,C=100μF an AC power supply with variable frequency is connected . Calculate the value of angular frequency of the source at which the circuit is in resonance and current at the same frequency . The V_("rms") value of voltage in the circuit is 220 V.
The correct Answer is:44.6rads−1,14.67A
To solve the problem step by step, let's break it down into two parts: finding the angular frequency at resonance and calculating the current at that frequency.
Step 1: Calculate the Angular Frequency at Resonance
In a series LCR circuit, resonance occurs when the inductive reactance (X_L) is equal to the capacitive reactance (X_C). The formulas for these reactances are:
- Inductive Reactance: XL=ωL
- Capacitive Reactance: XC=1ωC
At resonance, we have:
XL=XC
This leads to:
ωL=1ωC
Rearranging gives:
ω2=1LC
Thus, the angular frequency ω at resonance can be calculated as:
ω=1√LC
Now, substituting the given values:
- L=5H
- C=100μF=100×10−6F
Calculating ω:
ω=1√5×100×10−6
=1√5×0.0001
=1√0.0005
=10.02236
≈44.72rad/s
Step 2: Calculate the Current at Resonance
At resonance, the impedance Z of the circuit is equal to the resistance R:
Z=R=15Ω
The current Irms can be calculated using Ohm's law:
Irms=VrmsZ
Given:
- Vrms=220V
Substituting the values:
Irms=22015
≈14.67A
Final Answers
1. The angular frequency at which the circuit is in resonance is approximately 44.72rad/s.
2. The current at this frequency is approximately 14.67A.
- Capacitive Reactance: XC=1ωC
XL=XC
ωL=1ωC
ω2=1LC
ω=1√LC
- L=5H
- C=100μF=100×10−6F
ω=1√5×100×10−6
=1√5×0.0001
=1√0.0005
=10.02236
≈44.72rad/s
Z=R=15Ω
Irms=VrmsZ
- Vrms=220V
Irms=22015
≈14.67A
1. The angular frequency at which the circuit is in resonance is approximately 44.72rad/s.
2. The current at this frequency is approximately 14.67A.
Topper's Solved these Questions
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CONCEPTUAL QUESTIONS
Explore 25 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:TOUGH & TRICKY PROBLEMS
Explore 12 Videos
- ALTERNATING CURRENT Book:MODERN PUBLICATIONChapter:ALTERNATING CURRENT Exercise:CHAPTER PRACTICE TEST
Explore 16 Videos
- ATOMS Book:MODERN PUBLICATIONChapter:ATOMS Exercise:Chapter Practice Test
Explore 16 Videos
Similar Questions
A series LCR circuit with L=4.0h,C=100μF and R=60Ω is connected to a varialbe frequency 240 V source. Calcalate
(i) angular frequency of the source which drives the circuit in resonace,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductro at resonance.
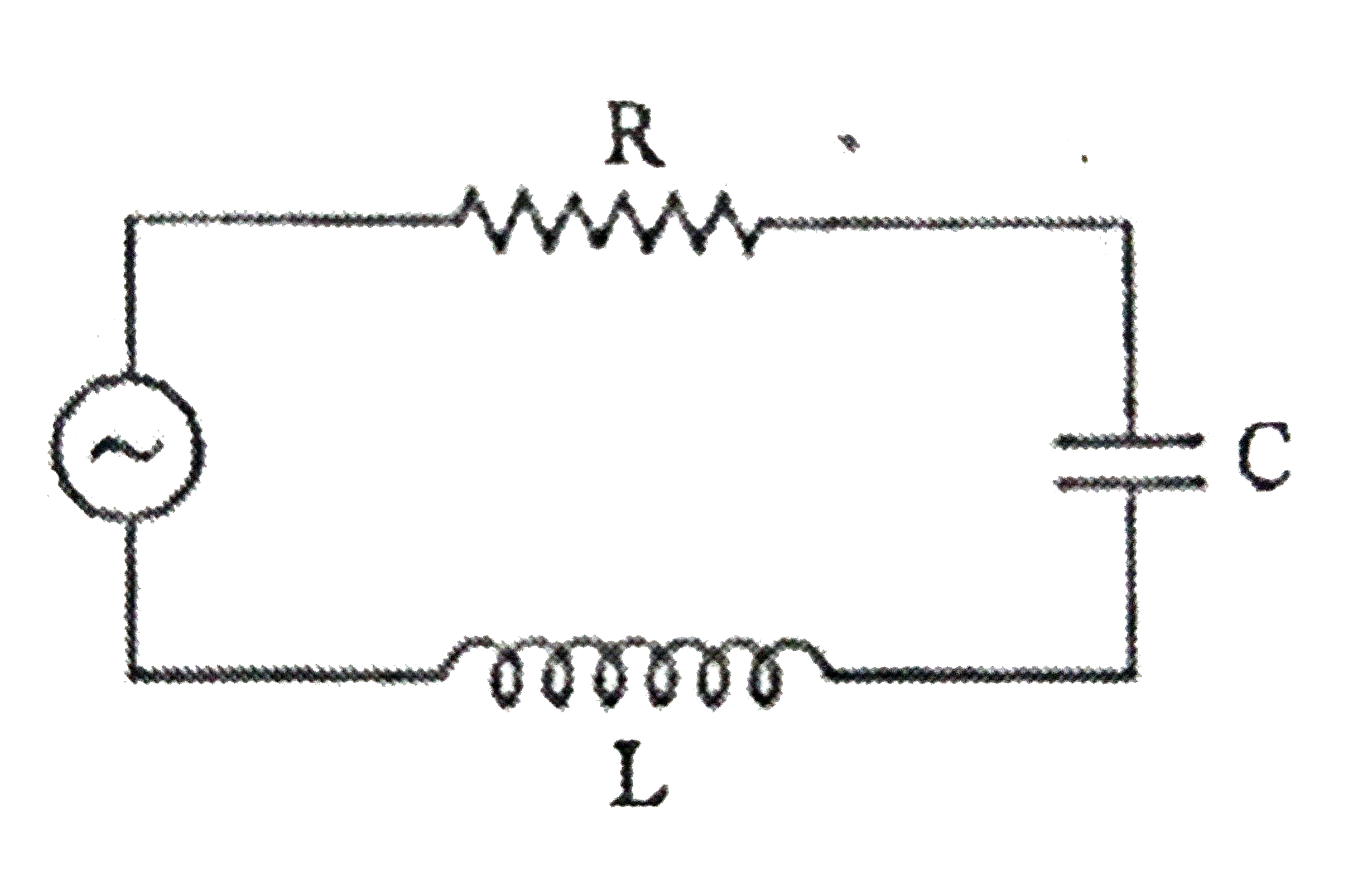
View SolutionThe figure shows a series LCR circuit with L=10.0H2,C=40μF,R=60Ω connected to a variable frequency 240 V source. Calculate
(i) The angular frequency of the source which drives the circuit at resonance.
(ii) The current at the resonating frequency.
(iii) The rms potential drop across the capacitor at resonance.
View Solution
Knowledge Check
A series LCR circuit with R=22Ω,L=1.5H and C=40μF is connected to a variable frequency 220 V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?
A2000 WB2200 WC2400 WD2500 W
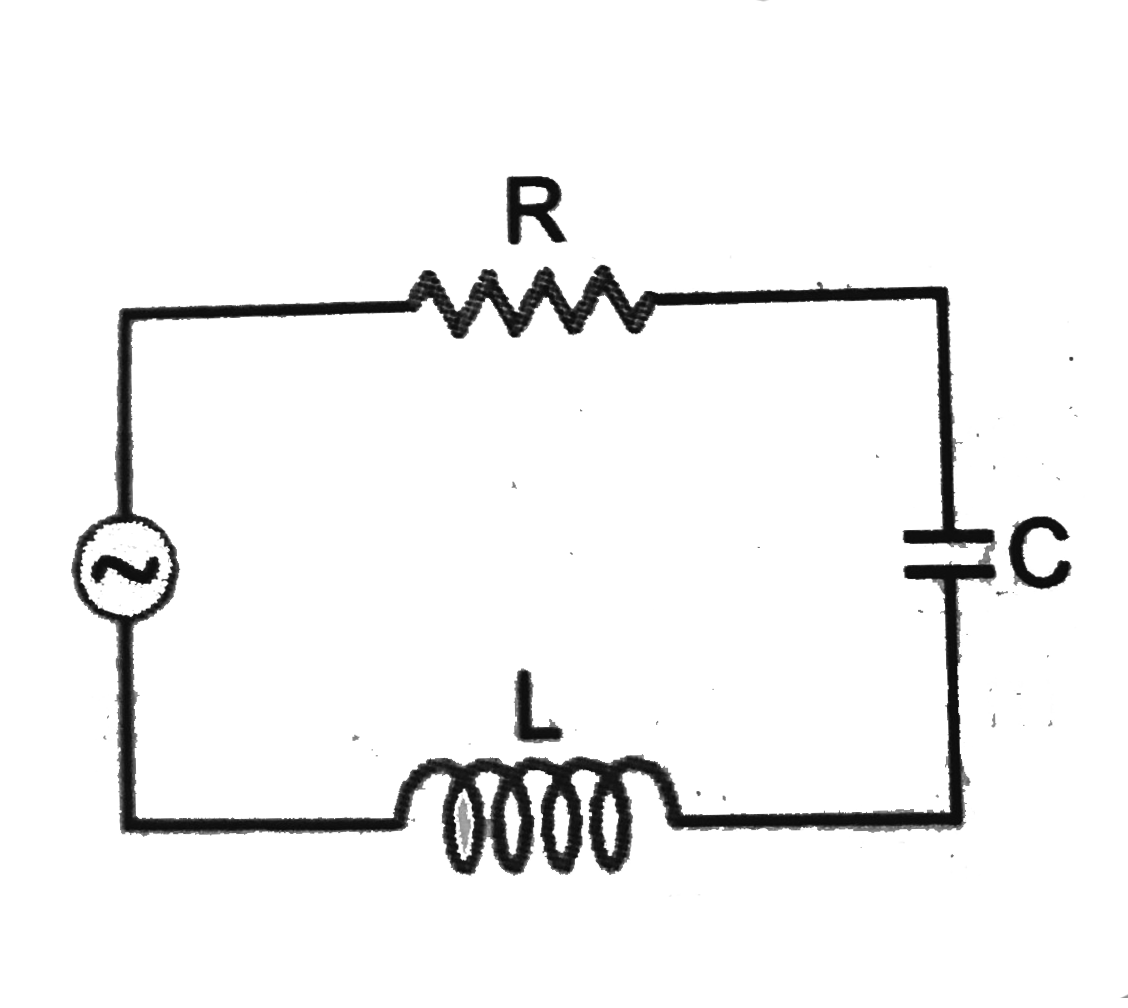
Fig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular freuquency of the source which drives the circuit at resonance.
(ii) Current at the resonanting frequency.
(iii) the rms pot. drop across the capacitor at resonance.
View SolutionA series L-C-R circuit with R=44Ω,C=8μFandL=50H is connected to a variable frequency 220 V ac suppy. Calculate angular frequency, impedance and current at resonance condition.
View SolutionIn a series LCR circuit with variable inductor 80 nF capacitor and 70 ohm resistance an AC source is connected . Calculate the value of inductor if current drawn into the circuit is maximum. The frequency of AC source is 1 kHz.
View SolutionA series LCR circuit with R=20Ω , L = 1.5 H and C = 35 μF is connected to a variable-frequency 200 V a.c. supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle ?
View SolutionA series LCR circuit with R=20Ω,L=1.5H and C=35μF is connected to a variable frequency 200V ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power in Kw transferred to the circuit in one complete cycle?
View SolutionA series LCR a.c. circuit has L = 2.0 H, C = 32 μF and R = 10 Ω.
(a) At what angular frequency of a.c. will it resonate ?
(b) Calculate the Q value of the circuit.
View SolutionA series LCR circuit containing 5.0 H inductor, 80μF capacitor and 40Ω resistor is connected to 230 V variable frequency ac source. The angular frequencies of the source at which power transfered to circuit is half the power at resonant angular frequency are likely to be.
View Solution

