(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig.
(b) Evaluate the induced emf in loop if the wire carries a current of 50 A and the loop has an instantaneous velocity υ=10ms−1 at the location x = 0.2 m, as shown. Take a = 0.1m and assume that the loop has a large resistance.
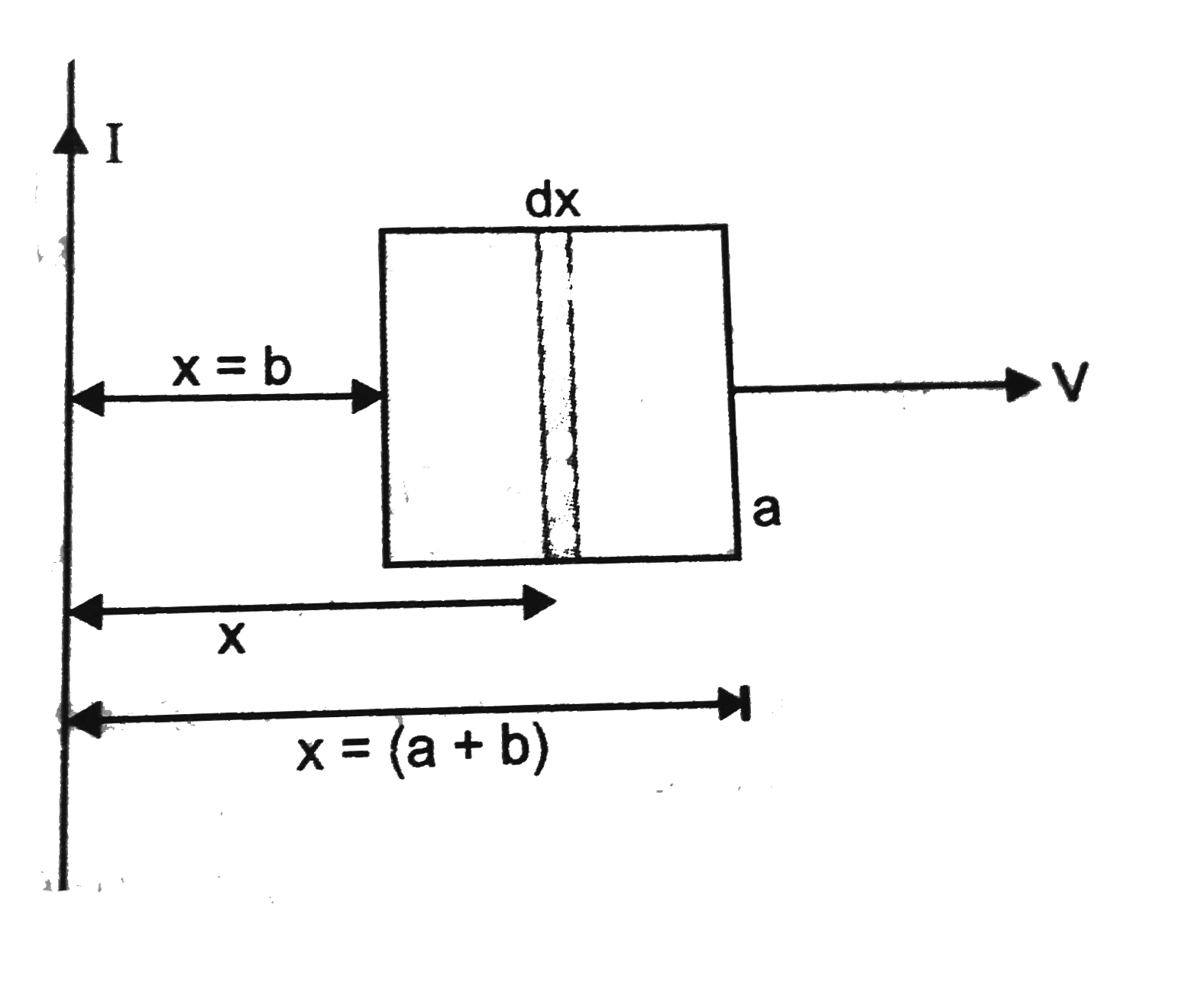
(a) Let us consider a small strip of thickness dr at a distance r from the straight wire as shown in the figure given below, assuming that the magnetic field is uniform over this slit.
Area of the strip, dA = adr .
∴ Magnetic field at a distance from the long straight current-carrying wire carrying current I is
B=μ0I2πr

So magnetic flux linked with this strip
dϕ=B×dA
or dϕ=μ0I2πr×adr
∴ Total magnetic flux linked with the whole square loop
ϕ=∫dϕ=∫r=x+ar=xμ0Ia2πrdr
=μ0Ia2π∫r=x+ar=xdrr
=μ0Ia2πIn[x+ax]
=μ0Ia2πIn[1+ax]
ϕ=MI⇒M=μ0a2πIn[1+ax]
(b) Given, current in the straight wire, 1 = 50 A,
Velocity of loop, v=10ms−1,
Distance between the wire and loop, x = 0.2 m,
Side of the square loop, a = 0.1 m
The induced emf is
ε=−dϕdt
=−ddt[μ0Ia2π{In(x + a) - Inx}]
=−μ0Ia2πr[1x+a−1x]dxdt
or ε=−μ0Ia2π[1x+a−1x]v
=−4π×10−7×50×0.12π×[10.2+0.1−10.2]×10
=−2×10−7×5×[−10.6]×10
=1.66×10−5V=1.7×10−5V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Very short answer type questions)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT EXEMPLAR PROBLEMS SUBJECTIVE QUESTIONS) (Short answer type questions)
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NCERT FILE (NCERT TEXTBOOK EXERCISE)
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Chapter Practice Test
15 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
Similar Questions
Find the mutual inductance between the straight wire and the square loop of figure.
View Solution(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side a as shown in Fig. 6.06.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s. Calculate the induced emf in the loop at the instant when x = 0.2 m. Take a = 0.1 m and assume that the loop has a large resistance.
View Solution
Knowledge Check
The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
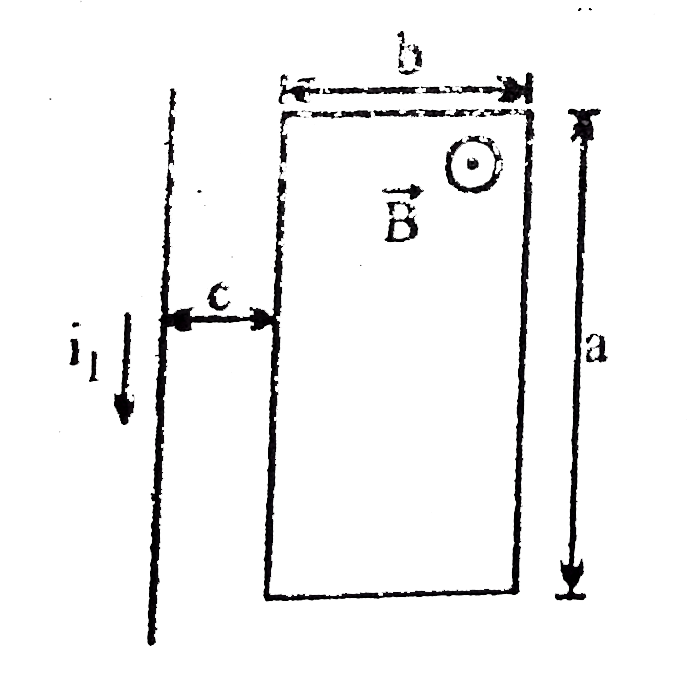 AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)
AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
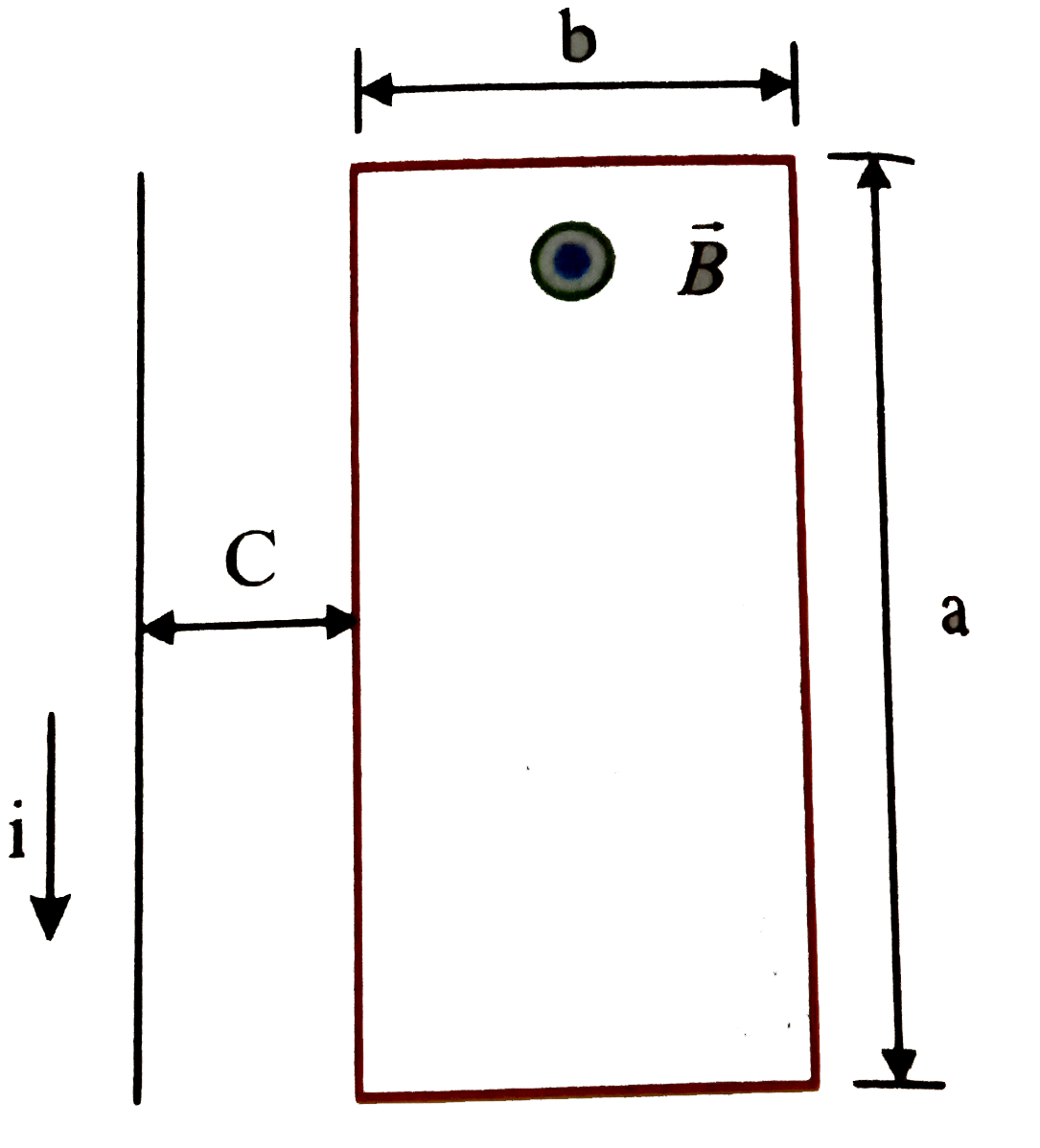 AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)
AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)A loop and an infinite wire are placed side by side as shown in the figure. If the current I in the wire is increased then the induced current in the loop is
 AclockwiseBanticlockwiseCzeroDcannot determine
AclockwiseBanticlockwiseCzeroDcannot determine
Find the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
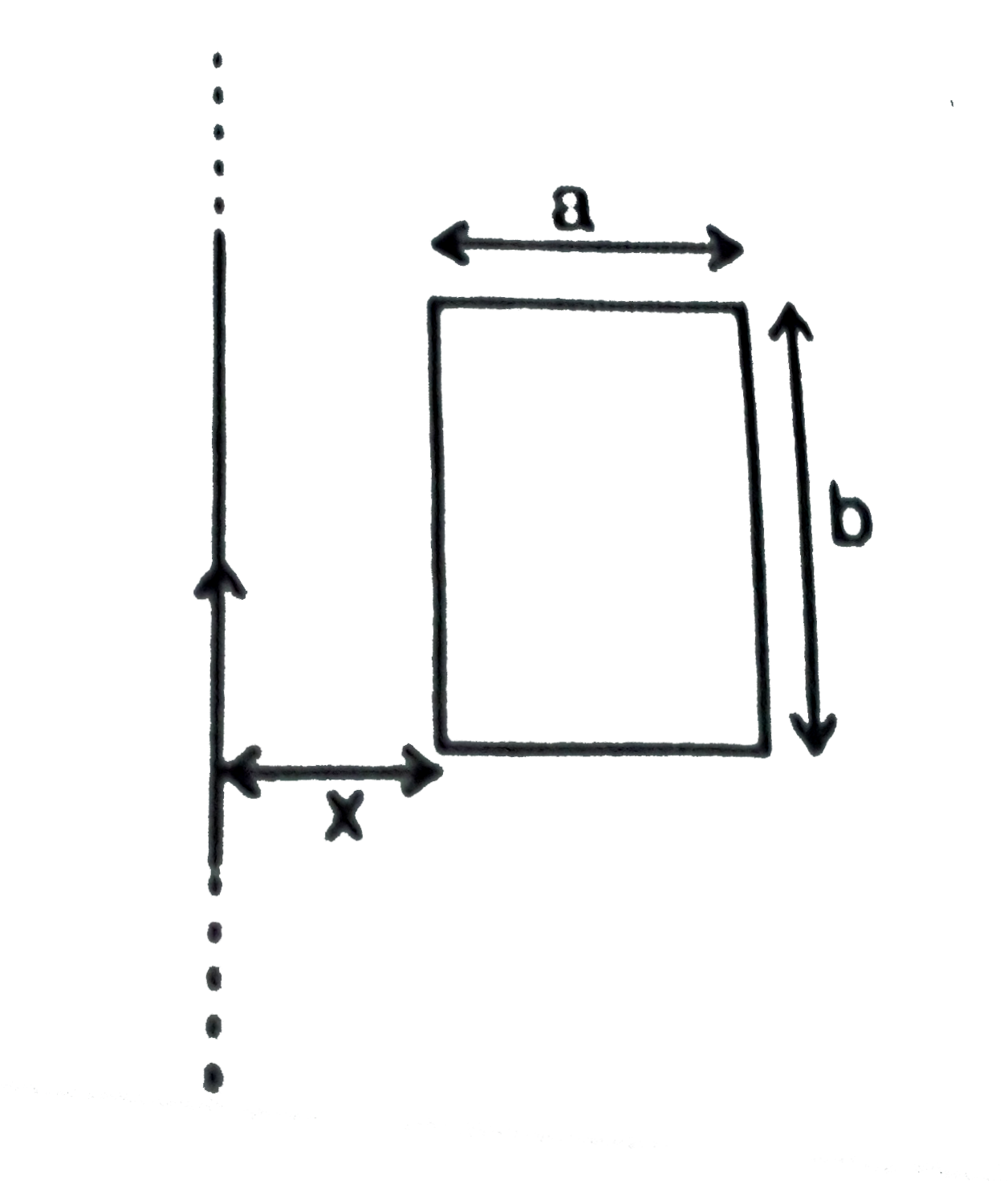
View SolutionThe induced emf in the loop, if the long wire carries a current of 50A and the loop has an instantaneous velocity v=10ms at the location x=0,2m as shown in figure is e microvolt. Caluclate 3ε (Take a=0.1m)
'(##CEN_KSR_PHY_JEE_CO23_E01_038_Q14##)'
View SolutionFigure shows a conducting loop placed near a long straight wire carrying a current i as shown, if the current increases continuously, find the direction of the induced current in the loop.

View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.

View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View Solution
