Question

A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness
$\delta =\frac{d}{N}$ .The dielectric constant of the $m^{th}$ layer is $K_m=K(1+\frac{m}{N})$. For a very large $N(<{10}^3),$ the capacitance C is $\alpha \left(\frac{k{\in }_{0}A}{d1n2}\right)$ .The value of $\alpha willbe.<br>$ [in _0 is the permittivity of free space ]

Answer

1

Explanation

First we need to convert this problem in the form of integration.
Refer following diagram:

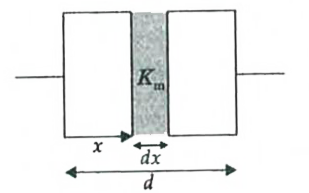
We have selected a segment of width dx at a distance x as shown in figure. But the question is given in terms of layers.
Here we can visualize `delta=d//N=dx`
Further `m^(th)` layer is bisically segment of width dx selected at distance x.
So we can write `m//N=x//d`
Hence `K_(m)=K(1+(m)/(N))=K(1+(x)/(d))`
Capacitance of the segment can be written as follows:
`dC=(K_(m)Aepsilon_(0))/(dx)`
`(1)/(C )=int (1)/(dC)= int_(0)^(d) (dx)/(K_(m)Aepsilon_(0))`
`rArr (1)/(C )=(1)/(KAepsilon_(0)) int_(0)^(d) (dx)/((1+(x)/(d)))`
`rArr (1)/(C )=(d)/(KA epsilon_(0))["In"(1+(x)/(d))]_(0)^(d)`
`rArr (1)/(C )=(d)/(KAepsilon_(0))["In "2-"In "1]`
`rArr (1)/(C )=("d In"2)/(KA epsilon_(0))`
`rArr C=(KA epsilon_(0))/("d In"2)`
On comparing with given result we can see that `alpha=1`.