A parallel plate capacitor of capacitance has spacing between two plates having area The region between the plates is filled with dielectric layers, parallel to its plates, each with thickness δ=dN. The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(>103), the capacitance Cisα(K∈0Adln2). Find the value of α.[∈0 is the permittivity of free space]
The correct Answer is:1.00
For verry large N, δ is verry small.Let it be dx
d=Nδ
x=mδ∴mN−dx
Capacitance of elemental capacitor
dc=Kmε0Aδ=K(1+xd)ε0Adx
Such capactors are connected in series
∴1c∫1dc∫20dKε0Add+x=dKε0A1n2

Knowledge Check
- Question 1 - Select One
A parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
A3CBC3C12 CDC6 - Question 1 - Select One
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1) - Question 1 - Select One
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2] - Question 1 - Select One
A parallel plate capacitor of capacitance C is charged to a potential V and then disconnected with the battery. If separation between the plates is decreased by 50% and the space between the plates is filled with a dielectric slab of dielectric constant K=10. then
AP.d. between the plates increases by 95%BP.d. between the plates decreases by 50%CP.d. between the plates increases by 50%DP.d. between the plates decreases by 95% - Question 1 - Select One
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF - Question 1 - Select One
A parallel plate capacitor with air between the plates has capacitance of 9pF. The separation between its plates is 'd'. The space between the plates is now filled with two dielectrics. One of the dielectrics has dielectric constant k1=3 and thickness d3 while the other one has dielectric constant k2=6 and thickness 2d3. Capacitance of the capacitor is now
A1.8 pFB45 pFC40.5 pFD20.25pF
Similar Questions
A parallel plate capacitor of capacitance C has spacing d between two plates having area A. The region between the plates is filled with N dielectric layers, parallel to its plates, each with thickness
δ=dN .The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(<103), the capacitance C is α(k∈0Ad1n2) .The value of αwillbe.<br> [in _0 is the permittivity of free space ]View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionTwo identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
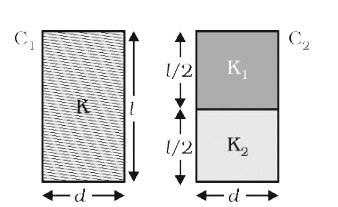 View Solution
View SolutionA parallel plate capacitor with air inbetween the paltes has a capacitance of 8 pF. The separation between the plates is now reduced by half and the space between them is filled with a medium of dielectric constant 5.
Calculate the new value of capacitance.View Solution

