Two identical capacitors of 10 pF each are connected is turn (i) in series and (ii) in parallel across a 20 V battery. Calculate the potential difference across each capacitor in the first case and charge acquired by each capacitor in the second case.
To solve the problem, we need to analyze the two configurations of the capacitors: first in series and then in parallel.
Step 1: Capacitors in Series
When capacitors are connected in series, the total capacitance (C_total) can be calculated using the formula:
1Ctotal=1C1+1C2
Given that both capacitors have the same capacitance of 10 pF:
1Ctotal=110pF+110pF=210pF=15pF
Thus, the total capacitance is:
Ctotal=5pF
Next, we calculate the total charge (Q) stored in the series configuration using the formula:
Q=Ctotal×V
Where V is the voltage across the battery (20 V):
Q=5pF×20V=100pC
Since the charge is the same across all capacitors in series, each capacitor will have a charge of:
Q1=Q2=100pC
Now, to find the potential difference (V) across each capacitor, we use the formula:
V=QC
For each capacitor:
V1=Q1C1=100pC10pF=10V
V2=Q2C2=100pC10pF=10V
Step 2: Capacitors in Parallel
When capacitors are connected in parallel, the voltage across each capacitor is the same and equal to the battery voltage (20 V). The charge on each capacitor can be calculated using the formula:
Q=C×V
For each capacitor:
Q1=C1×V=10pF×20V=200pC
Q2=C2×V=10pF×20V=200pC
Final Answers
- Potential difference across each capacitor in series: 10 V
- Charge acquired by each capacitor in parallel: 200 pC
When capacitors are connected in series, the total capacitance (C_total) can be calculated using the formula:
When capacitors are connected in parallel, the voltage across each capacitor is the same and equal to the battery voltage (20 V). The charge on each capacitor can be calculated using the formula:
- Potential difference across each capacitor in series: 10 V
- Charge acquired by each capacitor in parallel: 200 pC
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Competition file (MULTIPLE CHOICE QUESTIONS based on a given passage/comprehension)
Explore 17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Competition file (ASSERTION REASON TYPE QUESTIONS)
Explore 8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:Revision Exercises (Long Answer Questions)
Explore 13 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Find charge on each capacitor and potential difference across each capacitor .

View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View Solution
Knowledge Check
Two capacitors of capacitances 10μFand20μF are connected in series across a potential difference of 100V. The potential difference across each capacitor is respectively
A66.67 V, 33.33 VB60 V, 40 VC50 V, 50 VD90 V, 10 V
If A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionTwo capacitors of capacitance 6uF and 4uF are put in series across a 120V battery. What is the potential difference across the 4uF capacitor?
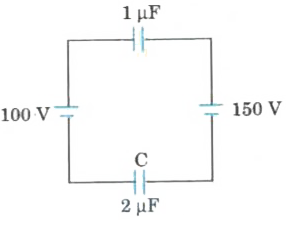
View SolutionTwo parallel plate capacitors of capacitances 1 pF and 2 pF are connected to the batteries of 100 V and 150 V as shown in the figure (r ). Calculate the potential difference across each capacitor.
View SolutionTwo identical resistors, each of resistance are connected in (i) series, and (ii) parallel, in turn to a battery of 6 V. Calculate the ratio of the power consumed in the combination of resistors in each case.
View SolutionTwo capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.
View SolutionTwo identical capacitors of 10 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination.
View SolutionTwo identical capacitors of 12 pF each are connected in series across a 50 V battery. Calculate the electrostatic energy stored in the combination. If these were connected in parallel across the same battery, find out the value of the energy stored in this combination.
View Solution

