Three point charges are arranged at the vertices of an equilateral triangle ABC of side l. Charges at A, B and C are +q, +4q and -6q, respectively.
(i) Calculate electric potential energy of this system.
(ii) Charge at A is moved to the midpoint of AB, charge at B is moved to midpoint of BC and charge at C is moved to midpoint of CA. Calculate electric potential energy of this system now.
(iii) What work is needed to shift the charges to new locations as described in part (ii)?
To solve the problem, we will break it down into three parts as specified in the question.
Part (i): Calculate the electric potential energy of the system.
1. Identify the charges and their positions:
- Charge at A: +q
- Charge at B: +4q
- Charge at C: −6q
- The distance between each pair of charges is l (the side of the equilateral triangle).
2. Formula for electric potential energy:
The electric potential energy U of a system of point charges is given by:
U=14πϵ0∑i<jQiQjrij
where Qi and Qj are the point charges and rij is the distance between them.
3. Calculate the pairwise potential energy contributions:
- Between A and B:
UAB=14πϵ0(+q)(+4q)l=4q24πϵ0l
- Between B and C:
UBC=14πϵ0(+4q)(−6q)l=−24q24πϵ0l
- Between C and A:
UCA=14πϵ0(−6q)(+q)l=−6q24πϵ0l
4. Sum the contributions:
U=UAB+UBC+UCA=4q24πϵ0l−24q24πϵ0l−6q24πϵ0l
U=(4−24−6)q24πϵ0l=−26q24πϵ0l
Part (ii): Calculate the electric potential energy of the new configuration.
1. New positions of charges:
- Charge at A moves to the midpoint of AB (let's call it P).
- Charge at B moves to the midpoint of BC (let's call it Q).
- Charge at C moves to the midpoint of CA (let's call it R).
2. Distance between new charges:
The distance between each pair of new charges (P, Q, R) is l2.
3. Calculate the new pairwise potential energy contributions:
- Between P and Q:
UPQ=14πϵ0(+q)(+4q)l2=8q24πϵ0l
- Between Q and R:
UQR=14πϵ0(+4q)(−6q)l2=−48q24πϵ0l
- Between R and P:
URP=14πϵ0(−6q)(+q)l2=−12q24πϵ0l
4. Sum the contributions:
U′=UPQ+UQR+URP=8q24πϵ0l−48q24πϵ0l−12q24πϵ0l
U′=(8−48−12)q24πϵ0l=−52q24πϵ0l
Part (iii): Calculate the work needed to shift the charges.
1. Work done (W):
The work done in moving the charges is equal to the change in potential energy:
W=U′−U
Substituting the values we found:
W=−52q24πϵ0l−−26q24πϵ0l
W=−52q2+26q24πϵ0l=−26q24πϵ0l
2. Interpretation:
A negative work indicates that energy is released when moving the charges to the new configuration.
Summary of Results:
- (i) Electric potential energy of the system: U=−26q24πϵ0l
- (ii) Electric potential energy of the new configuration: U′=−52q24πϵ0l
- (iii) Work done to shift the charges: W=−26q24πϵ0l
- Charge at A: +q
- Charge at B: +4q
- Charge at C: −6q
- The distance between each pair of charges is l (the side of the equilateral triangle).
The electric potential energy U of a system of point charges is given by:
U=14πϵ0∑i<jQiQjrij
where Qi and Qj are the point charges and rij is the distance between them.
- Between A and B:
UAB=14πϵ0(+q)(+4q)l=4q24πϵ0l
- Between B and C:
UBC=14πϵ0(+4q)(−6q)l=−24q24πϵ0l
- Between C and A:
UCA=14πϵ0(−6q)(+q)l=−6q24πϵ0l
U=UAB+UBC+UCA=4q24πϵ0l−24q24πϵ0l−6q24πϵ0l
U=(4−24−6)q24πϵ0l=−26q24πϵ0l
- Charge at A moves to the midpoint of AB (let's call it P).
- Charge at B moves to the midpoint of BC (let's call it Q).
- Charge at C moves to the midpoint of CA (let's call it R).
The distance between each pair of new charges (P, Q, R) is l2.
- Between P and Q:
UPQ=14πϵ0(+q)(+4q)l2=8q24πϵ0l
- Between Q and R:
UQR=14πϵ0(+4q)(−6q)l2=−48q24πϵ0l
- Between R and P:
URP=14πϵ0(−6q)(+q)l2=−12q24πϵ0l
U′=UPQ+UQR+URP=8q24πϵ0l−48q24πϵ0l−12q24πϵ0l
U′=(8−48−12)q24πϵ0l=−52q24πϵ0l
The work done in moving the charges is equal to the change in potential energy:
W=U′−U
Substituting the values we found:
W=−52q24πϵ0l−−26q24πϵ0l
W=−52q2+26q24πϵ0l=−26q24πϵ0l
A negative work indicates that energy is released when moving the charges to the new configuration.
- (i) Electric potential energy of the system: U=−26q24πϵ0l
- (ii) Electric potential energy of the new configuration: U′=−52q24πϵ0l
- (iii) Work done to shift the charges: W=−26q24πϵ0l
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 1
Explore 10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 2
Explore 21 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
Three point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View Solution
Knowledge Check
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2Equal charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
Aq4πε0a2B√2q4πε0a2C√3q4πε0a2Dq2πε0a2
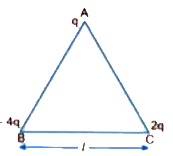
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
View SolutionTwo point charges +6qand−8q are placed at the vertices B and C of an equilateral triangle ABC of side a. Obtain an expression for magnitude and direction of resultant electric field at the vertex A due to these two charges.
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionΔABC is an equilateral triangle, AB = 6. The points P, Q and Rare midpoints of AB, BC and CA respectively. The perimeter of PBCR is
View Solution

