Two point charges +6qand−8q are placed at the vertices B and C of an equilateral triangle ABC of side a. Obtain an expression for magnitude and direction of resultant electric field at the vertex A due to these two charges.
To find the magnitude and direction of the resultant electric field at vertex A due to the point charges +6q at vertex B and -8q at vertex C of an equilateral triangle ABC with side length a, we can follow these steps:
Step 1: Identify the Charges and Their Positions
- We have two charges:
- Charge at B: +6q
- Charge at C: −8q
- The distance between A and B (and A and C) is equal to the side length of the triangle, which is a.
Step 2: Calculate the Electric Field Due to Each Charge at Point A
The electric field E due to a point charge is given by the formula:
E=14πϵ0|Q|r2
where Q is the charge and r is the distance from the charge to the point where the field is being calculated.
Electric Field at A due to Charge at B (+6q):
EAB=14πϵ06qa2
Electric Field at A due to Charge at C (-8q):
EAC=14πϵ08qa2
Step 3: Determine the Directions of the Electric Fields
- The electric field EAB due to the positive charge at B points away from B towards A.
- The electric field EAC due to the negative charge at C points towards C (attracting A).
Step 4: Analyze the Geometry of the Electric Fields
Since triangle ABC is equilateral, the angle between the electric fields EAB and EAC is 120∘.
Step 5: Calculate the Magnitude of the Resultant Electric Field
Using the law of cosines for vector addition, the magnitude of the resultant electric field ER can be calculated as:
ER=√E2AB+E2AC+2EABEACcos(120∘)
Substituting cos(120∘)=−12:
ER=
⎷(14πϵ06qa2)2+(14πϵ08qa2)2+2(14πϵ06qa2)(14πϵ08qa2)(−12)
Step 6: Simplify the Expression
Let E=14πϵ0qa2:
EAB=6E,EAC=8E
Now substituting:
ER=√(6E)2+(8E)2−6E⋅8E
=√36E2+64E2−48E2
=√52E2=2√13E
Step 7: Substitute Back to Get the Final Expression
Thus, the resultant electric field at point A is:
ER=2√13q4πϵ0a2
Step 8: Determine the Direction of the Resultant Electric Field
To find the direction, we can use the components of the electric fields:
- The angle β can be calculated using the components of EAB and EAC.
Using trigonometric relationships, we can find:
tan(β)=EABsin(30∘)EAC−EABcos(30∘)
This will give us the angle of the resultant electric field with respect to the line connecting A and C.
Final Result
The magnitude of the resultant electric field at vertex A is:
ER=2√13q4πϵ0a2
And the direction can be calculated using the angle β.
- We have two charges:
- Charge at B: +6q
- Charge at C: −8q
- The distance between A and B (and A and C) is equal to the side length of the triangle, which is a.
The electric field E due to a point charge is given by the formula:
E=14πϵ0|Q|r2
where Q is the charge and r is the distance from the charge to the point where the field is being calculated.
EAB=14πϵ06qa2
EAC=14πϵ08qa2
- The electric field EAB due to the positive charge at B points away from B towards A.
- The electric field EAC due to the negative charge at C points towards C (attracting A).
Since triangle ABC is equilateral, the angle between the electric fields EAB and EAC is 120∘.
Using the law of cosines for vector addition, the magnitude of the resultant electric field ER can be calculated as:
ER=√E2AB+E2AC+2EABEACcos(120∘)
Substituting cos(120∘)=−12:
ER=
⎷(14πϵ06qa2)2+(14πϵ08qa2)2+2(14πϵ06qa2)(14πϵ08qa2)(−12)
Let E=14πϵ0qa2:
EAB=6E,EAC=8E
Now substituting:
ER=√(6E)2+(8E)2−6E⋅8E
=√36E2+64E2−48E2
=√52E2=2√13E
Thus, the resultant electric field at point A is:
ER=2√13q4πϵ0a2
To find the direction, we can use the components of the electric fields:
- The angle β can be calculated using the components of EAB and EAC.
tan(β)=EABsin(30∘)EAC−EABcos(30∘)
This will give us the angle of the resultant electric field with respect to the line connecting A and C.
The magnitude of the resultant electric field at vertex A is:
ER=2√13q4πϵ0a2
And the direction can be calculated using the angle β.
Similar Questions
Two point charges +q and -2qare placed at the vertices B and C of an equilateral triangle ABC of side 'a' as shown in Obtain the expression for
The magnitude ,
(b)
The direction of the resultant electric field at the vertex A due to these two charges.
(c)
View SolutionTwo point charges +q and -2q are placed at the vertices B and C of an equilateral triangle ABC of side 'a' as shown Obtain the expession for (i) the magnitude ,and (ii) the direction of the resultant electric field at the vertex A due to these two charges .
View Solution
Knowledge Check
Equal charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
Aq4πε0a2B√2q4πε0a2C√3q4πε0a2Dq2πε0a2Three point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2 qxB3√2qxC3 qxD2√3qxThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2qxB3√2qxC3qxD2√3qx
Three point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
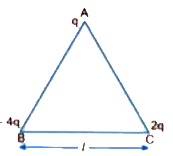
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View Solution

