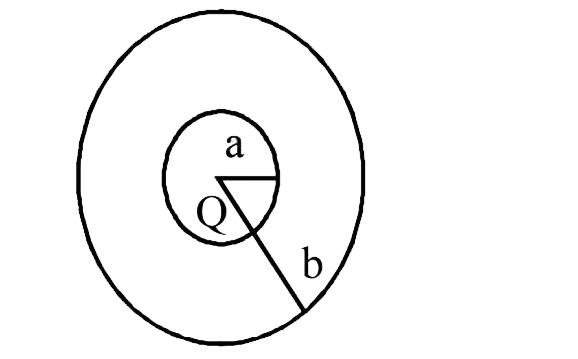
The region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density $ρ = \frac{A}{r}$ , where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:

$\frac{Q}{2 π a^{2}}$

$\frac{Q}{2 π (b^{2} - a^{2})}$

$\frac{2 Q}{π (a^{2} - b^{2})}$

$\frac{2 Q}{π a^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A solid sphere of radius R has a volume charge density $ρ = ρ_{0} r^{2}$ (where $ρ_{0}$ is a constant ans r is the distance from centre). At a distance x from its centre (for $x < R$ ), the electric field is directly proportional to :
A $1 / x^{2}$
B $1 / x$
C $x^{3}$
D $x^{2}$
An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density $ρ = \frac{A}{r}$ , where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
A $\frac{A R}{8 ε_{0}}$
B $\frac{A R}{4 ε_{0}}$
C $\frac{A R}{ε_{0}}$
D $\frac{A R}{2 ε_{0}}$
A system consists of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density $ρ = \frac{α}{r}$ , where $α$ is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
A $\frac{α}{2 ε_{0}}$
B $\frac{2}{α ε_{0}}$
C $2 π α R^{2}$
DNone of these