Two non-conducting spheres of radii R1 and R2 and carrying uniform volume charge densities +ρ and −ρ respectively are placed such that they partially overlapping region.
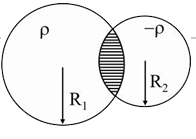
Electric field intensity is zero
The magnitude and direction of electric field intensity are uniform
The magnitude of electric field intensity is uniform but the direction is changing from point to point
None
The correct Answer is:B

→E=ρ→r13ε0−ρ→r23ε0=ρ3ε0(→r1−→r2)=ρ→r03ε0
Here →r0 is a constant vector which joins the centres of both the spheres . Hence , the electric field intensity inside the overlapping region is uniform.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ) )
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Numerical Problems )
7 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Two non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.

View SolutionThere are two nonconducting spheres having uniform volume charge densities ρ and −ρ . Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take →d=O1−→O2.

The electric field →E in the overlapped region is
View Solution
Knowledge Check
Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
A(a) −4B(b) −3325C(c) 3225D(d) 4Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
Ar21/r22Br22/r21Cr1/r2Dr2/r1Two conducting spheres of radii r1 and r2 are charged to the same surface charge density . The ratio of electric field near their surface is
Ar21/r22Br22/r21Cr1/r2D1:1
There are two nonconducting spheres having uniform volume charge densities ρ and −ρ . Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in Fig.2.125. Take →d=O1−→O2.

The potential difference ΔV between the centres of the two spheres for d=R is
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionTwo conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionA charge Q has been divided on two concentric conducting spheres of radii R1 and R2(R1>R1) such that the surface charge densities on both the spheres are equal. The potential at their common centre is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solution
