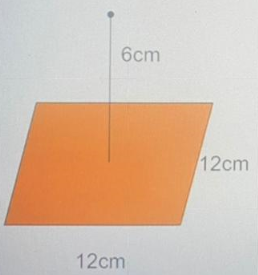
Surface subtends a solid angle of π on a point charge +q. Electric flux due to point charge, associated with the given surface, is
q/ε0
q/2ε0
q/4ε0
q/8ε0
The correct Answer is:C
To solve the problem of finding the electric flux due to a point charge +q associated with a surface that subtends a solid angle of π, we can follow these steps:
Step 1: Understand the Concept of Electric Flux
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) of the surface projected in the direction of the field. Mathematically, it is given by:
Φ=∫→E⋅d→A
For a point charge, we can also use Gauss's law, which states:
Φ=qencϵ0
where qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Step 2: Determine the Total Electric Flux for a Complete Sphere
When a point charge +q is enclosed by a surface (like a sphere), the total electric flux through that surface is:
Φtotal=qϵ0
This total flux corresponds to a solid angle of 4π steradians, which is the solid angle for a complete sphere.
Step 3: Relate Solid Angle to Electric Flux
The total solid angle around a point charge is 4π steradians. Since the surface in question subtends a solid angle of π steradians, we can find the fraction of the total flux that corresponds to this solid angle.
Step 4: Calculate the Electric Flux for the Given Solid Angle
The electric flux associated with the solid angle π can be calculated as:
Φ=Solid Angle4π×Φtotal
Substituting the values we have:
Φ=π4π×qϵ0=14×qϵ0=q4ϵ0
Final Answer
Thus, the electric flux due to the point charge +q associated with the given surface that subtends a solid angle of π is:
Φ=q4ϵ0
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) of the surface projected in the direction of the field. Mathematically, it is given by:
Φ=∫→E⋅d→A
For a point charge, we can also use Gauss's law, which states:
Φ=qencϵ0
where qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
When a point charge +q is enclosed by a surface (like a sphere), the total electric flux through that surface is:
Φtotal=qϵ0
This total flux corresponds to a solid angle of 4π steradians, which is the solid angle for a complete sphere.
The total solid angle around a point charge is 4π steradians. Since the surface in question subtends a solid angle of π steradians, we can find the fraction of the total flux that corresponds to this solid angle.
The electric flux associated with the solid angle π can be calculated as:
Φ=Solid Angle4π×Φtotal
Substituting the values we have:
Φ=π4π×qϵ0=14×qϵ0=q4ϵ0
Thus, the electric flux due to the point charge +q associated with the given surface that subtends a solid angle of π is:
Φ=q4ϵ0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ) )
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Numerical Problems )
7 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
Find the total flux due to charge q associated with the given hemispherical surface
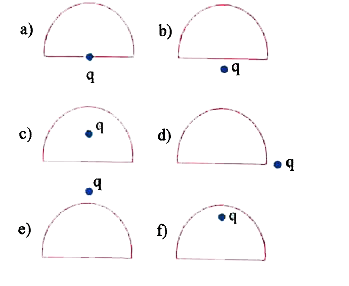 A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0
A(a)q2ε0,(b)0,(c)qε0,(d)0,(e)0(f)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0(f)qε0C(a)q2ε0,(b)qε0,(c)0,(d)qε0,(e)0(f)qε0D(a)0,(b)q2ε0,(c)0(d)qε0,(e)qε0(f)qε0Find the total flux due to charge qassociated with the given hemisphercal surface
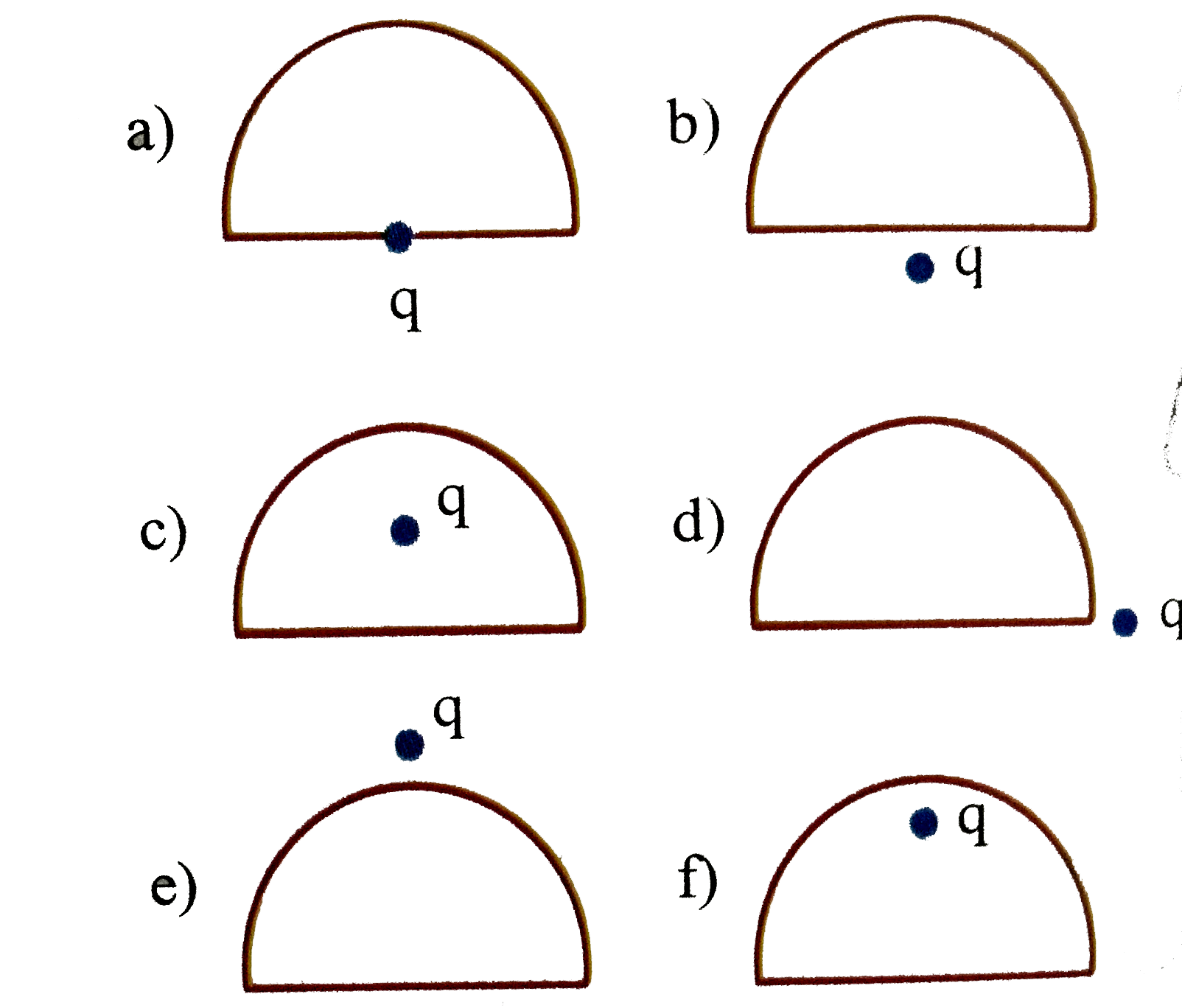 Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0
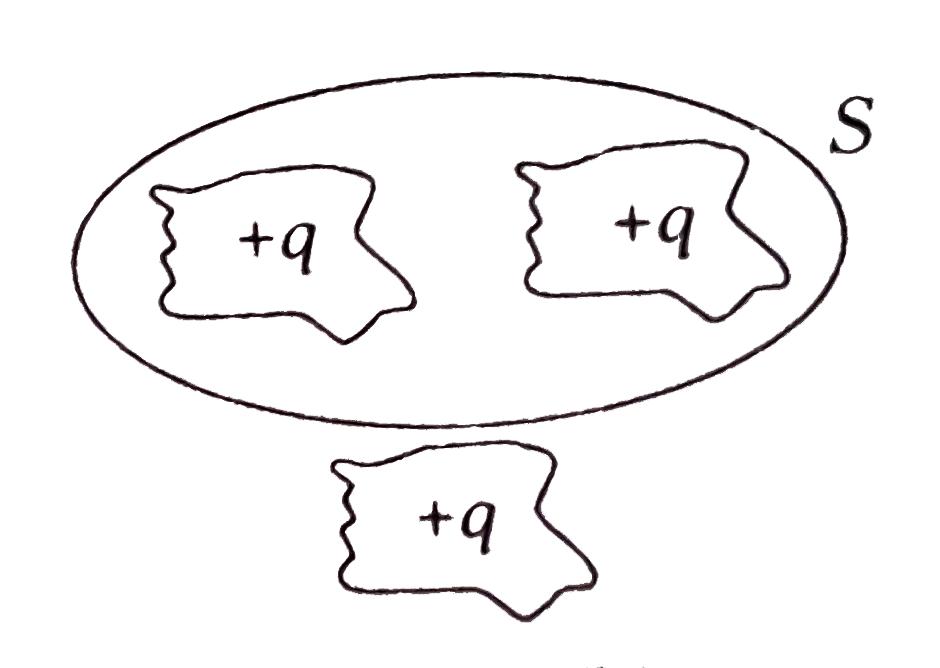
Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0The flux of electric field due to these charges through the surface S is
 A2qε0B3qε0C−5qε0Dqε0
A2qε0B3qε0C−5qε0Dqε0
Shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is
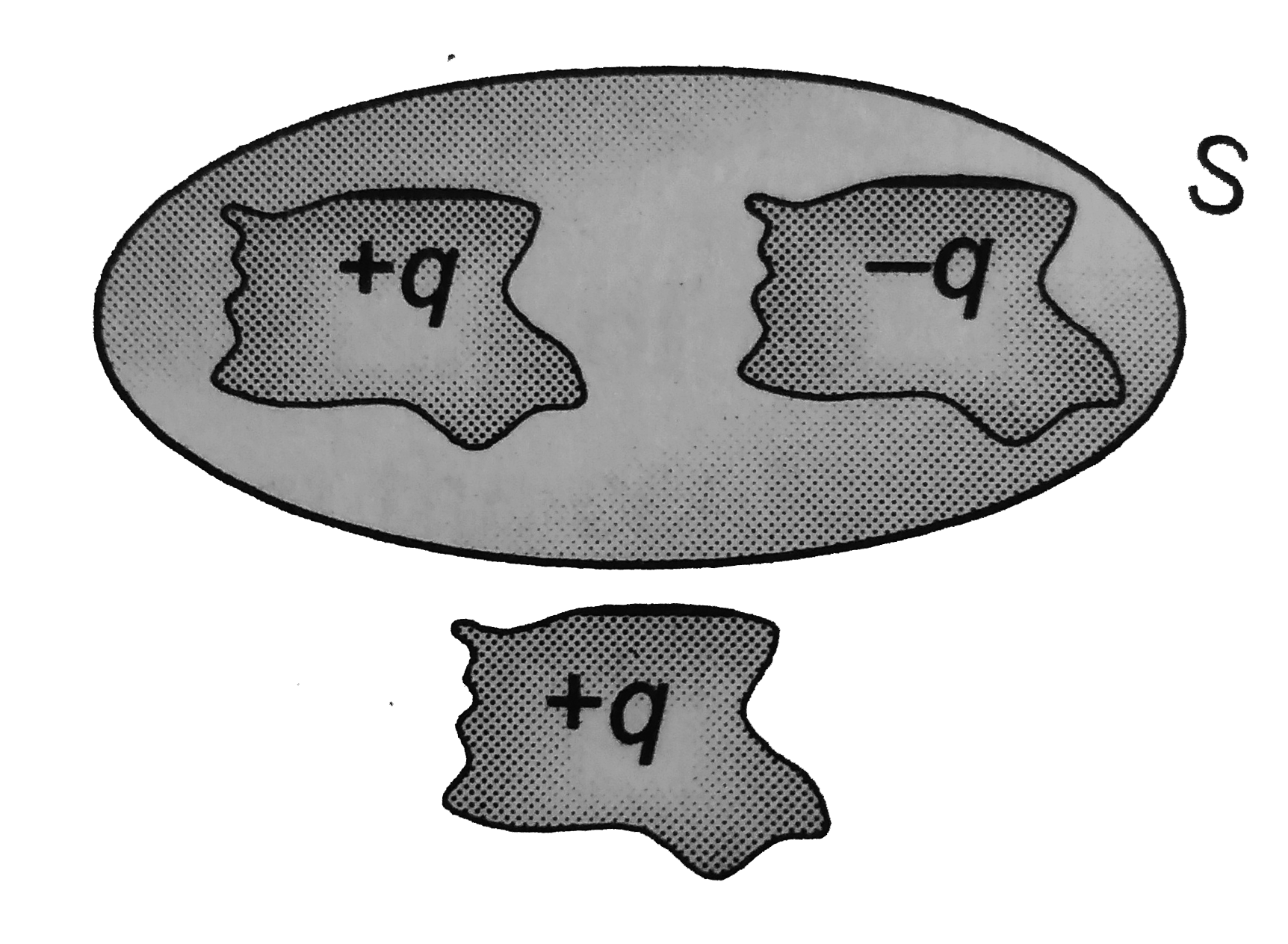
View SolutionFigure shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is
View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux is unit of volt -m associated with the curved surface B, the flux linked with the plane surface A in the same units will be

View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be
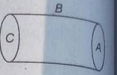
View SolutionA hollow cylinder has a charge q coulomb within it. If ϕ is the electric flux in unit of voltmeter associated with the curved surface B, the flux linked with the plane surface A in unit of voltmeter will be

View Solution