Two unequal and opposite charges are kept fixed at a distance. What is the number of points in space where electric Field intensity is zero due to this system?
0
1
2
None
The correct Answer is:B
To solve the problem of finding the number of points in space where the electric field intensity is zero due to two unequal and opposite charges, we can follow these steps:
Step 1: Understand the System
We have two charges, Q1 (positive) and Q2 (negative), where |Q1|>|Q2|. The charges are fixed at a distance r apart.
Step 2: Analyze the Electric Field
The electric field E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
Step 3: Identify Possible Locations for Zero Electric Field
1. Between the Charges: If we take a point between the two charges, the electric field due to Q1 will point away from Q1 (outward), and the electric field due to Q2 will point towards Q2 (inward). Since both fields are in the same direction, they cannot cancel each other out. Thus, there is no point between the charges where the electric field is zero.
2. Outside the Charges: We need to check the regions outside the line joining the two charges:
- To the left of Q1: Here, the electric field due to Q1 will point away from Q1 (to the left) and the electric field due to Q2 will point towards Q2 (to the left as well). Since both fields point in the same direction, they cannot cancel each other out.
- To the right of Q2: Here, the electric field due to Q1 will point away from Q1 (to the right) and the electric field due to Q2 will point towards Q2 (to the right). Again, both fields point in the same direction, so they cannot cancel each other out.
Step 4: Conclusion
Since we have established that there is no point between the charges and no point outside the charges where the electric fields can cancel each other, we conclude that there is only one point in space where the electric field intensity is zero, and that point is located on the line joining the two charges, closer to the smaller charge Q2.
Final Answer
The number of points in space where the electric field intensity is zero due to this system is 1.
---
We have two charges, Q1 (positive) and Q2 (negative), where |Q1|>|Q2|. The charges are fixed at a distance r apart.
The electric field E due to a point charge is given by the formula:
E=k|Q|r2
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge to the point where the electric field is being calculated.
1. Between the Charges: If we take a point between the two charges, the electric field due to Q1 will point away from Q1 (outward), and the electric field due to Q2 will point towards Q2 (inward). Since both fields are in the same direction, they cannot cancel each other out. Thus, there is no point between the charges where the electric field is zero.
- To the left of Q1: Here, the electric field due to Q1 will point away from Q1 (to the left) and the electric field due to Q2 will point towards Q2 (to the left as well). Since both fields point in the same direction, they cannot cancel each other out.
- To the right of Q2: Here, the electric field due to Q1 will point away from Q1 (to the right) and the electric field due to Q2 will point towards Q2 (to the right). Again, both fields point in the same direction, so they cannot cancel each other out.
Since we have established that there is no point between the charges and no point outside the charges where the electric fields can cancel each other, we conclude that there is only one point in space where the electric field intensity is zero, and that point is located on the line joining the two charges, closer to the smaller charge Q2.
The number of points in space where the electric field intensity is zero due to this system is 1.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ) )
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Numerical Problems )
7 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
Knowledge Check
Two charges of same polarity are kept fixed at a distance. What is the number of points in space where the electric field intensity due to this system is zero?
A1, if charges are of name magnitudeB2, if charges are of unequal magnitudeC2D1Two charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
Ar(1+√3) from 3e chargeBr(1+√3) from e chargeCr(1−√3) from 3e chargeDr1+√13 from e chargeTwo charge 9e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is :
A(r1+√3) from 9e chargeB(r1+√1/3) from 9e chargeC(r1−√3) from 3e chargeD(r1+√1/3) from 3e charge
Assertion: If there is a system of two unequal point charges of any polarity then there is one and only one point in space around it where the electric field intensity is zero.
Reason: The direction of electric field intensity at a point is away from the positive charge and towards the negative charge, along the line joining the charge and location where electric field intensity is to be calculated.
View SolutionAn electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
When point P lies on the equatorial plan of the electric dipole, electric field due to -q is ?
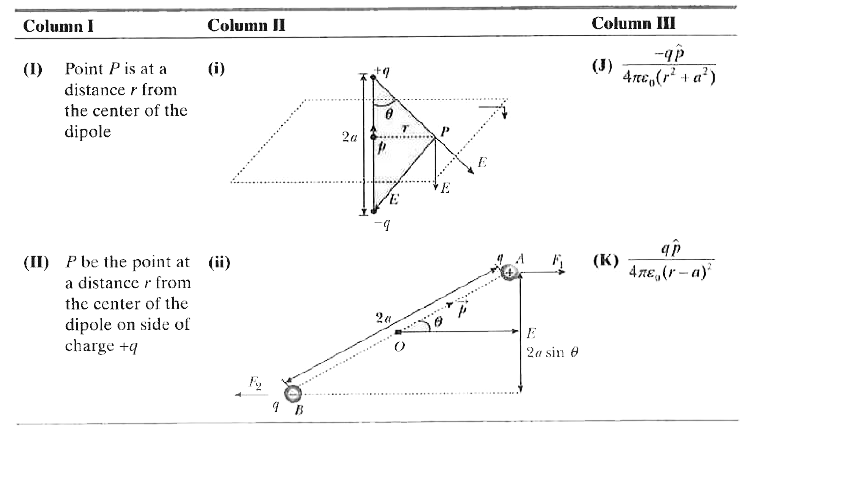
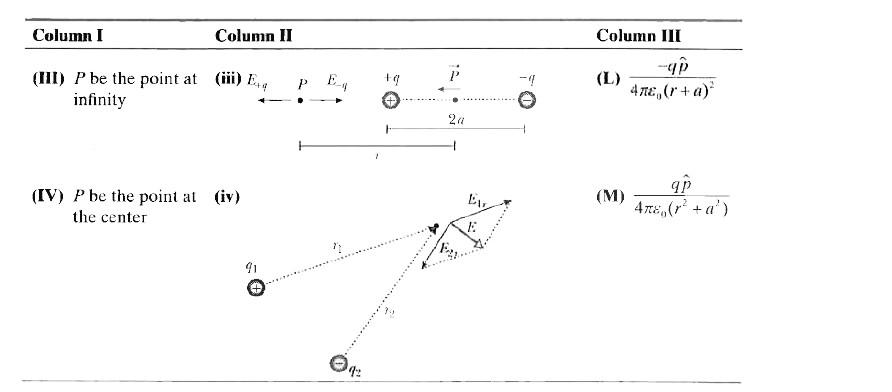
View SolutionAn electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
when point P lies on the equatorial plane of the electric dipole, electric field due to +q is ?
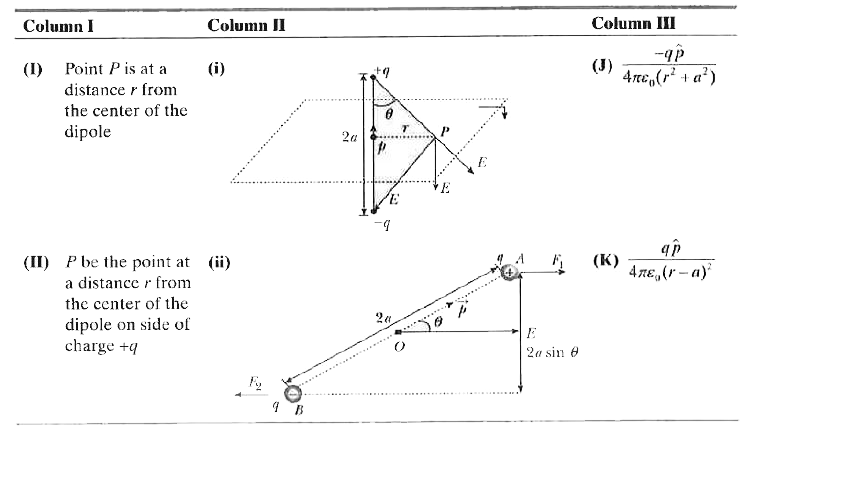
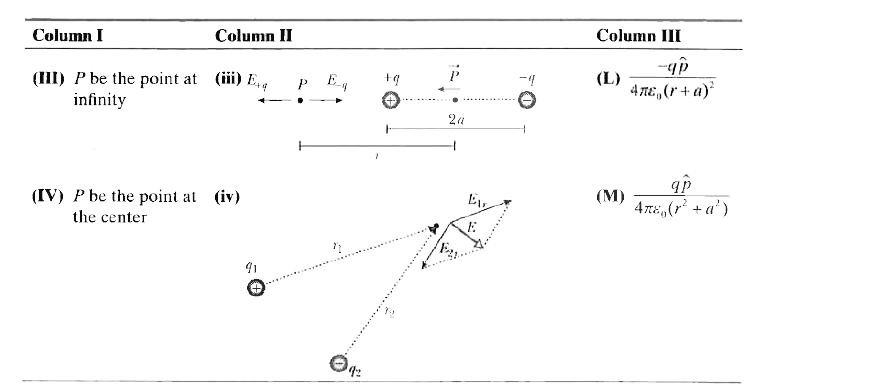
View SolutionAn electric dipole is the combination of two equal and opposite charges q and -q, respectively, separated by distance 2a. There are different points where we can find electric field due to the electric dipole. In the given table, column 1 shows different positions of point where we have to find electric field due to dipole, column 2 shows the figure of dipole with different positions of point where we have to find the electric field and column 3 shows the value or final formula of the electric field of different positions of the point.
When point P lies on the axis of the electric dipole, electric field due to -q is ?


View SolutionIn the diagram shown electric field intensity will be zero at a point.

View Solution
