There is a long straight wire, uniformly charged over length. A negatively charged point mass in ceiling around the wire under its electrostatic attraction. The linear speed of point mass is
Inversely proportional to the radius of circle
Directly proportional to the radius of circle
Independent of the radius
Unpredictable due to insufficient information
The correct Answer is:C
To find the linear speed of a negatively charged point mass moving in a circular path around a long straight wire with uniform charge density, we can follow these steps:
1. Understand the Setup:
- We have a long straight wire with a uniform linear charge density λ.
- A negatively charged point mass m with charge −q is moving in a circular path of radius d around this wire.
2. Electric Field Due to the Wire:
- The electric field E at a distance d from an infinitely long charged wire is given by:
E=2kλd
- Here, k is Coulomb's constant.
3. Force on the Point Mass:
- The electrostatic force FE acting on the negatively charged mass due to the electric field is:
FE=E⋅|q|=2kλd⋅q
- Since the charge is negative, the direction of the force will be opposite to the direction of the electric field.
4. Centripetal Force Requirement:
- For the point mass to move in a circular path, the electrostatic force must provide the necessary centripetal force:
FE=mv2d
- Here, v is the linear speed of the mass.
5. Equating Forces:
- Set the electrostatic force equal to the centripetal force:
2kλd⋅q=mv2d
6. Cancel d:
- Since d appears in both terms, we can cancel it out:
2kλq=mv2
7. Solve for v:
- Rearranging the equation gives:
v2=2kλqm
- Taking the square root yields:
v=√2kλqm
8. Conclusion:
- The linear speed v of the point mass is independent of the radius d of the circular path.
Final Expression:
v=√2kλqm
- We have a long straight wire with a uniform linear charge density λ.
- A negatively charged point mass m with charge −q is moving in a circular path of radius d around this wire.
- The electric field E at a distance d from an infinitely long charged wire is given by:
E=2kλd
- Here, k is Coulomb's constant.
- The electrostatic force FE acting on the negatively charged mass due to the electric field is:
FE=E⋅|q|=2kλd⋅q
- Since the charge is negative, the direction of the force will be opposite to the direction of the electric field.
- For the point mass to move in a circular path, the electrostatic force must provide the necessary centripetal force:
FE=mv2d
- Here, v is the linear speed of the mass.
- Set the electrostatic force equal to the centripetal force:
2kλd⋅q=mv2d
- Since d appears in both terms, we can cancel it out:
2kλq=mv2
- Rearranging the equation gives:
v2=2kλqm
- Taking the square root yields:
v=√2kλqm
- The linear speed v of the point mass is independent of the radius d of the circular path.
v=√2kλqm
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ) )
26 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - COMPETITION FILE ( Objective Question (BA.MCQ))
3 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Revision Exercises (Numerical Problems )
7 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
There is a particle A with positive charge q1 and mass m. There is another particle B with negative charge q2 and mass m. Particles A and B are moving along circular paths under electrostatic attraction in such a manner that separation between them is d and location of their centre of mass is centre of circular path. What will be the angular velocity of particles?
View SolutionAn indinitely long positively charged wire has a linear charge density λcm−1. An electron is revolving around the wire as its center with a constant velocity in a circular plane perpendicular to the wire. Deduce the expression for KE of electron. Plot a graph of K.E as a function of charge density λ.
View Solution
Knowledge Check
When a body becomes negatively charged, its mass
AdecreasesBincreasesCremains the sameDNone of theseA point charge -q is moving around another charge Q under the electrostatic attraction. If the path followed is elliptical, then
AThe angular momentum of charge -q remains constantBThe linear momentum of charge -q remains constantCThe angular speed of the charge -q remains constantDThe linear speed of the charge -q remains constantTwo semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -
 A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λr
A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λr
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
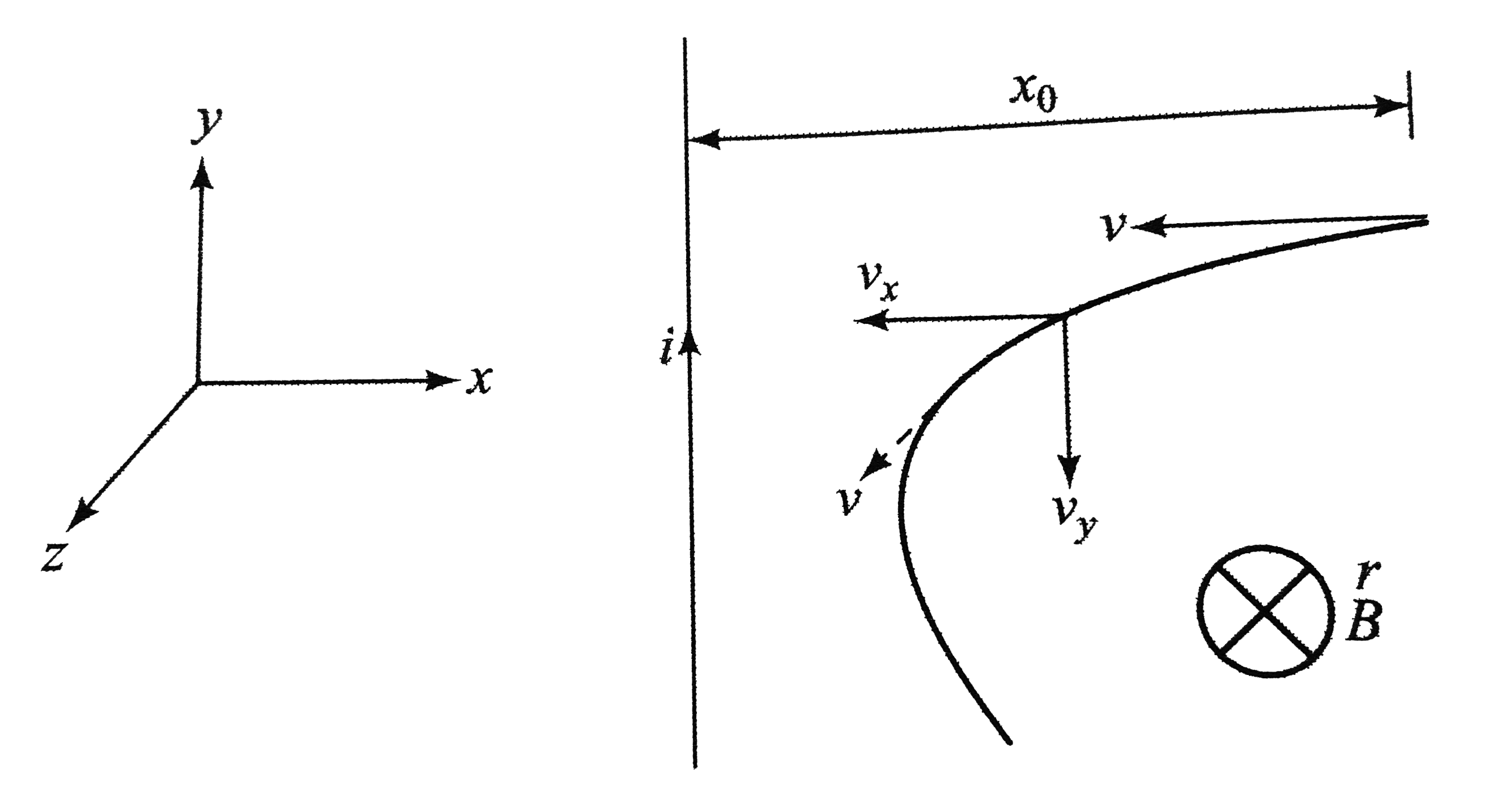

View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View SolutionA uniformly charged sphere has radius R and charge Q on it. A negatively charged particle having mass m and charge – q shoots out of the surface of the sphere with speed V. The minimum speed (V0) for which the particle escapes the attraction of the sphere may be called as escape speed. Will the value of V0 depend on magnitude of q? [Recall that escape speed of a body from the surface of the earth does not depend on its mass].
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
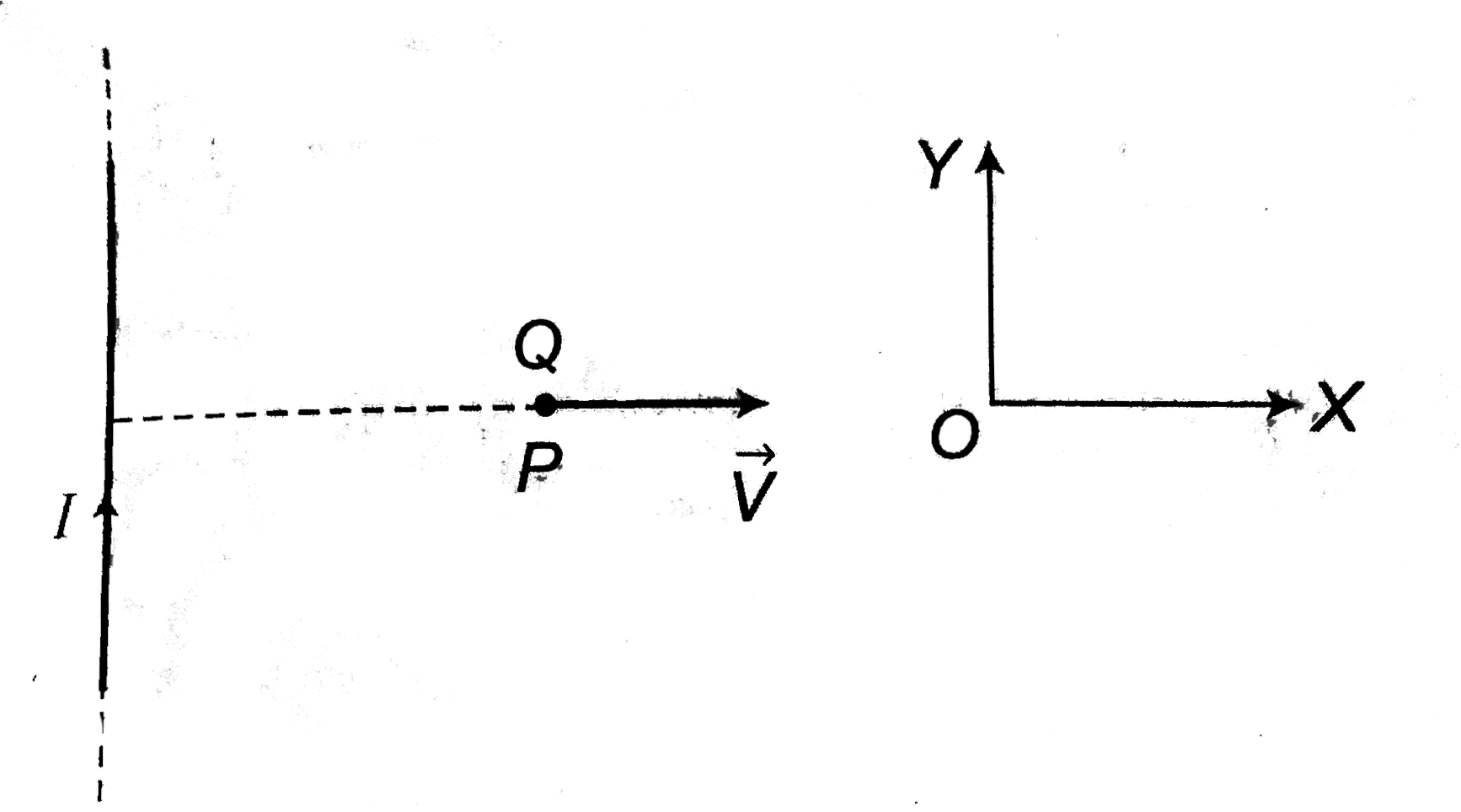
View Solution
