Two infinitely long line charges having charge density $λ$ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and $λ q > 0$ Neglect gravity. Find the time period.

Video Solution

Text Solution

Verified by Experts

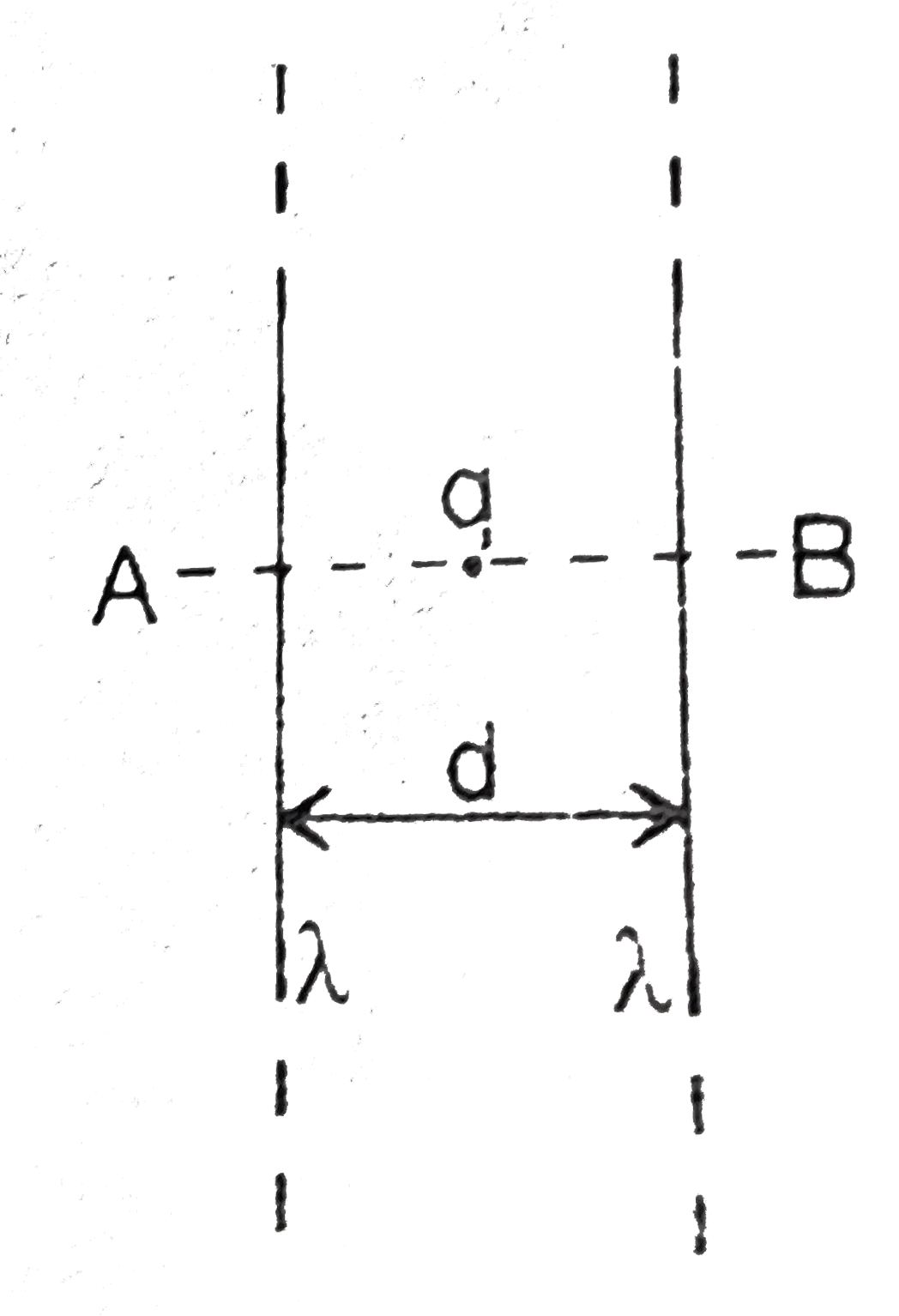
In the given figure the centre of AB is equilibrium position for a charged particle, because both charges apply the same repulsion on the particle of placed at this point. But when the particle is displaced towards one of the charges then its distance decreases from that charge but increases from other . The greater repulsion of near charge moves back the particle to its equilibrium, and subsequently the particle starts oscillating . Let a be the acceleration of particle when it is at displaced position as shown in the figure.

$m a = F_{1} - F_{2}$
Using Coulomb.s law , we can rewrite the above equation as follows :
$m a = \frac{1}{4 π ε_{0}} \frac{Q q}{{(d - x)}^{2}} - \frac{1}{4 π ε_{0}} \frac{Q q}{{(d + x)}^{2}}$
$\Rightarrow a = \frac{Q q}{4 π ε_{0} m} [\frac{1}{{(d - x)}^{2}} - \frac{1}{{(d + x)}^{2}}]$
$\Rightarrow a = \frac{Q q}{4 π ε_{0} m} [\frac{4 x d}{{(d^{2} x^{2})}^{2}}]$
For x < < d , we can neglect $x^{2}$ in comparison to $d^{2}$ . We get the following :
$\Rightarrow a = \frac{Q q}{π ε_{0} m d^{3}} x$
$\Rightarrow a = ω^{2} x$
$ω = \sqrt{\frac{Q q}{π ε_{0} m d^{3}}}$
Acceleration is proportional to displacement and always towards the centre O, hence it is S.H.M. Its time period is given by :
$T = \frac{2 π}{ω} \Rightarrow T = 2 π \sqrt{\frac{π ε_{0} m d^{3}}{Q q}}$
$\Rightarrow T = \sqrt{\frac{4 π^{3} ε_{0} m d^{3}}{Q q}}$

Updated on:21/07/2023

Two infinite plane parallel sheets separated by a distance d have equal and opposite uniform charge densities o. Electric field at a point between the sheets is
A $\frac{σ}{2 ε_{0}}$
B $\frac{σ}{ε_{0}}$
Czero
Ddepends on the location of the point
For an infinite line of charge having linear charge density $λ$ lying along x-axis the work done in moving a charge $q$ form $C$ to $A$ along $C A$ is

A $\frac{q λ}{2 π ε_{0}} In 2$
B $\frac{q λ}{2 π ε_{0}} In \sqrt{2}$
C $\frac{q λ}{4 π ε_{0}} In 2$
D $\frac{q λ}{2 π ε_{0}} In (0.5)$
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities $σ$ . Electric field at a point between the sheets is
A $\frac{σ}{2 ε_{0}}$
B $\frac{σ}{ε_{0}}$
Czero
Ddepends on the location of the point