Two electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance x(x<<d) perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : (m = mass of charged particle)
(2q2πε0md3)12
(πε0md32q2)12
(q22πε0md3)12
(2πε0md3q2)12
The correct Answer is:C
Step by step video, text & image solution for Two electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance x (x lt lt d) perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : (m = mass of charged particle) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:(SECTION - B)
Explore 10 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS (SECTION A)
Explore 60 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:PHYSICS (SECTION-B)
Explore 10 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Two charges −q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced at the mid-point is placed slightly by x(x<<d) perpendicular to the line joining the two fixed charges as shown in Fig. Show that q will perform simple harmonic oscillarion of time period.
T=[8π3∈0md3q2]1/2
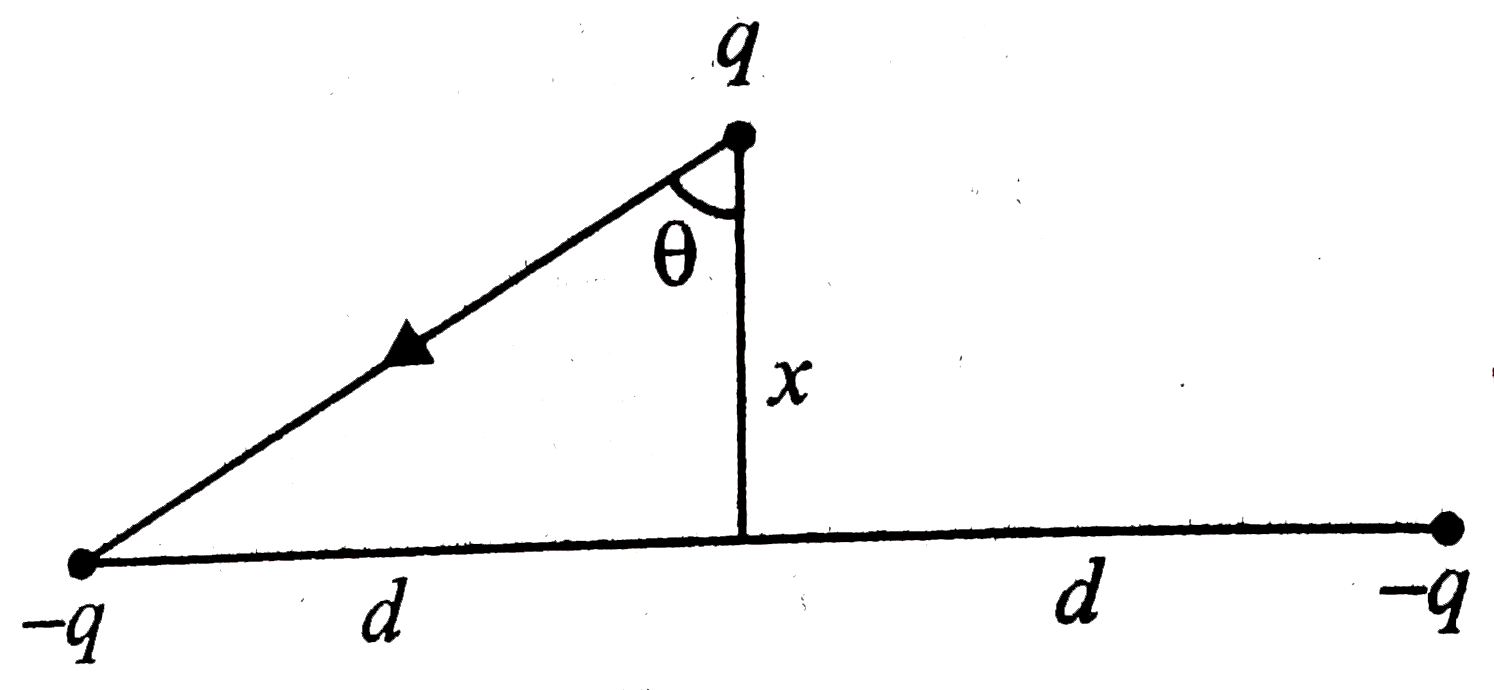
View SolutionTwo electrons are fixed at a seperation of 2d from each other.A proton is placed at the mid point and displaced slightly in a direction perpendicular to line joining the two electrons. Find frequency of oscillation of proton
View Solution
Knowledge Check
Two masses of mass m each are fixed at a separation distance of 2d. A small mass ms placed midway, when displaced slightly, starts oscillating. Then :
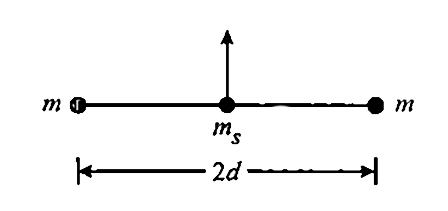 AFrequency of simple harmonic motion is given by 12π√4Gmd3BFrequency of simple harmonic motion is given by 12π√2Gmd3CAccleration of the mass ms, is given by Gmd2DTime period of vibration is 2π√GM(2d)3
AFrequency of simple harmonic motion is given by 12π√4Gmd3BFrequency of simple harmonic motion is given by 12π√2Gmd3CAccleration of the mass ms, is given by Gmd2DTime period of vibration is 2π√GM(2d)3Two equal charges are separated by a distance d. A third charge placed on a perpendicular bisector at x distance will experience maximum coulomb force when
Ax=d√2Bx=d2Cx=d2√2Dx=d2√3Two point charges +9e and +e are kept at a distance 'a' from each other. A third charge is placed at a distance 'x' from +9e on the line joining the above two charges. For the third charge to be in equilibrium 'x' is
A3a/4B3a/2Ca/2Da/4
Two points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
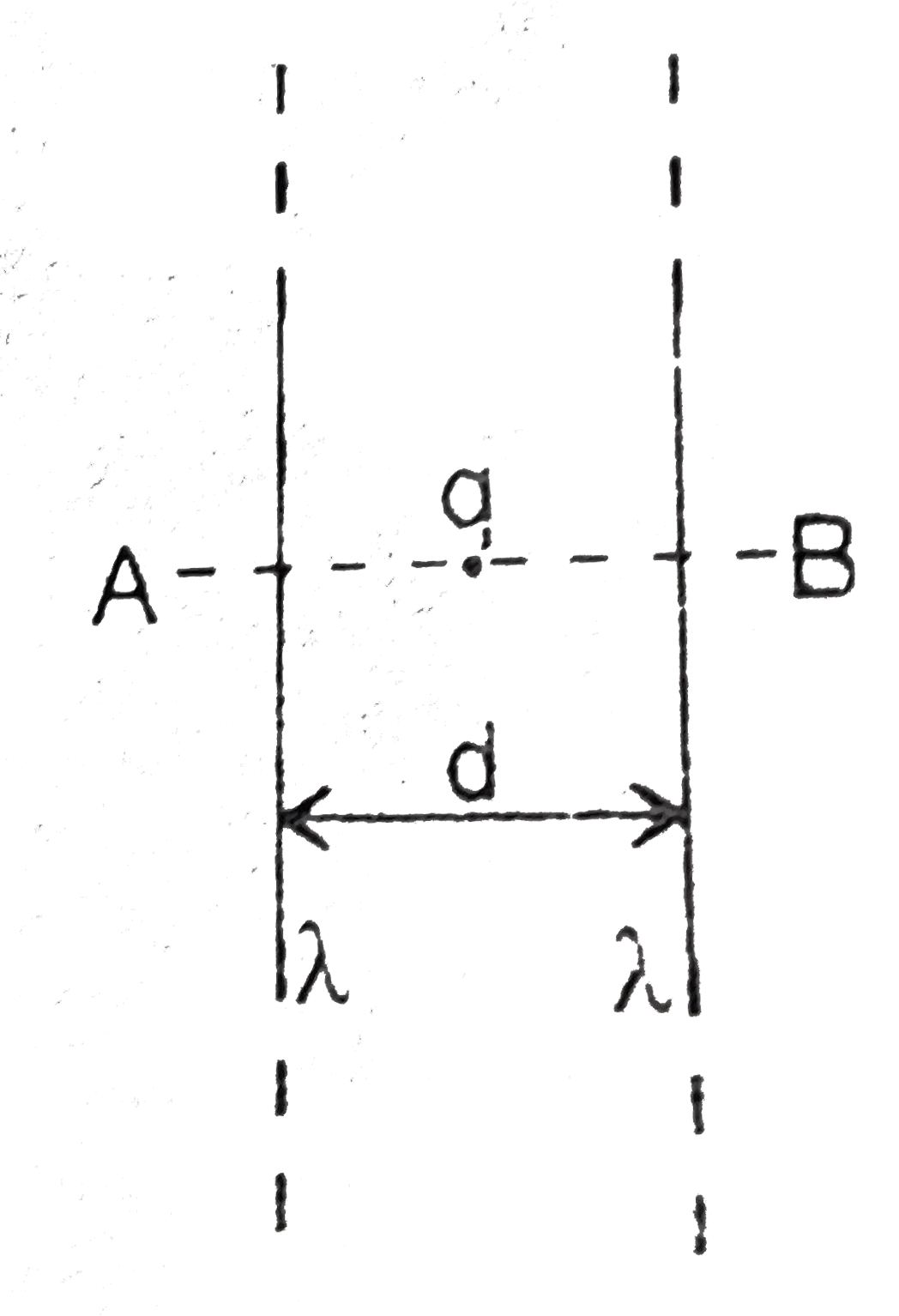
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionTwo particles A and B having equal charges are placed at distance d apart. A third charged particle placed on the perpendicular bisector at a distance x will experience the maximum Coulomb’s force when :
View SolutionTwo point masses, each equal to M, are placed a distance 2a apart. Show that a small mass m placed midway between them on the line joining them will be in equilibrium and if it is slightly displaced from this position along the line perpendicular to the line joining the masses, it will execute simple harmonic oscillations. Calculate the frequnency of these oscillations.
View SolutionTwo positive point charges , each Q , are fixed at separation d. A third charge q is placed in the middle. Describe the equilibrium of the third charge.
View Solution