Why do we always get electric field intensity near a charged metallic surface of magnitude twice of the electric field intensity near a thin sheet of charge with same surface charge density as of metal plate?
To understand why the electric field intensity near a charged metallic surface is twice that of a thin sheet of charge with the same surface charge density, we can break down the explanation into clear steps:
1. Understanding Electric Field Due to a Single Sheet of Charge:
- For a single infinite sheet of charge with surface charge density σ, the electric field E produced by this sheet is given by the formula:
E=σ2ϵ0
- This electric field is directed away from the sheet if the charge is positive and towards the sheet if the charge is negative.
2. Applying Gauss's Law:
- To derive the electric field due to a single sheet of charge, we can use Gauss's Law, which states:
ΦE=Qinϵ0
- For a Gaussian surface that encloses one side of the sheet, the total electric flux ΦE is equal to E⋅A (where A is the area of the Gaussian surface). The charge enclosed Qin is σA.
3. Calculating the Electric Field:
- Setting the electric flux equal to the charge enclosed gives:
E⋅A=σAϵ0
- Simplifying this, we find:
E=σ2ϵ0
4. Electric Field Due to a Charged Metallic Surface:
- A charged metallic surface, on the other hand, has charges distributed on its surface. For a charged metallic plate, the electric field E1 near the surface is due to the charges on both sides of the plate.
- Since the charges reside on the surface of the metallic plate, there are effectively two sheets of charge contributing to the electric field.
5. Calculating the Total Electric Field Near the Metallic Surface:
- Each side of the metallic plate contributes an electric field of σ2ϵ0. Therefore, the total electric field E1 near the metallic surface is:
E1=σ2ϵ0+σ2ϵ0=σϵ0
6. Comparing the Electric Fields:
- Let E2 be the electric field near a thin sheet of charge (which is σ2ϵ0).
- We find that:
E1=2E2
- Thus, the electric field intensity near the charged metallic surface is twice that of the thin sheet of charge.
Conclusion:
The electric field intensity near a charged metallic surface is twice that of a thin sheet of charge with the same surface charge density because the metallic surface has charges on both sides, effectively creating two layers of charge that contribute to the electric field.
- For a single infinite sheet of charge with surface charge density σ, the electric field E produced by this sheet is given by the formula:
E=σ2ϵ0
- This electric field is directed away from the sheet if the charge is positive and towards the sheet if the charge is negative.
- To derive the electric field due to a single sheet of charge, we can use Gauss's Law, which states:
ΦE=Qinϵ0
- For a Gaussian surface that encloses one side of the sheet, the total electric flux ΦE is equal to E⋅A (where A is the area of the Gaussian surface). The charge enclosed Qin is σA.
- Setting the electric flux equal to the charge enclosed gives:
E⋅A=σAϵ0
- Simplifying this, we find:
E=σ2ϵ0
- A charged metallic surface, on the other hand, has charges distributed on its surface. For a charged metallic plate, the electric field E1 near the surface is due to the charges on both sides of the plate.
- Since the charges reside on the surface of the metallic plate, there are effectively two sheets of charge contributing to the electric field.
- Each side of the metallic plate contributes an electric field of σ2ϵ0. Therefore, the total electric field E1 near the metallic surface is:
E1=σ2ϵ0+σ2ϵ0=σϵ0
- Let E2 be the electric field near a thin sheet of charge (which is σ2ϵ0).
- We find that:
E1=2E2
- Thus, the electric field intensity near the charged metallic surface is twice that of the thin sheet of charge.
The electric field intensity near a charged metallic surface is twice that of a thin sheet of charge with the same surface charge density because the metallic surface has charges on both sides, effectively creating two layers of charge that contribute to the electric field.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Tough & Tricky Problems
Explore 20 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Ncert File (Textbook Exercise)
Explore 34 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Practice Problems
Explore 88 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
Knowledge Check
The electric intensity at a point near a charged conductor of surface charge density σ is
AE=σ/∈0kBE=σ∈0kCE=σ/2∈0kDE=σ2The electric field intensity on the surface of a charged conductor is
AzeroBdirected normally to the surfaceCdirected tangentially to the surfaceDdirected along 45∘ to the surfaceThe electric field intensity on the surface of a charged conductor is
AzeroBdirected normally to the surfaceCdirected tangentially to the surfaceDdirected along 45∘ to the surface
The electric field at a point near an infinite thin sheet of a charged conductor is .
View SolutionThe electric field on two sides of a thin sheet of charge is shown in the figure. The charge density on the sheet is
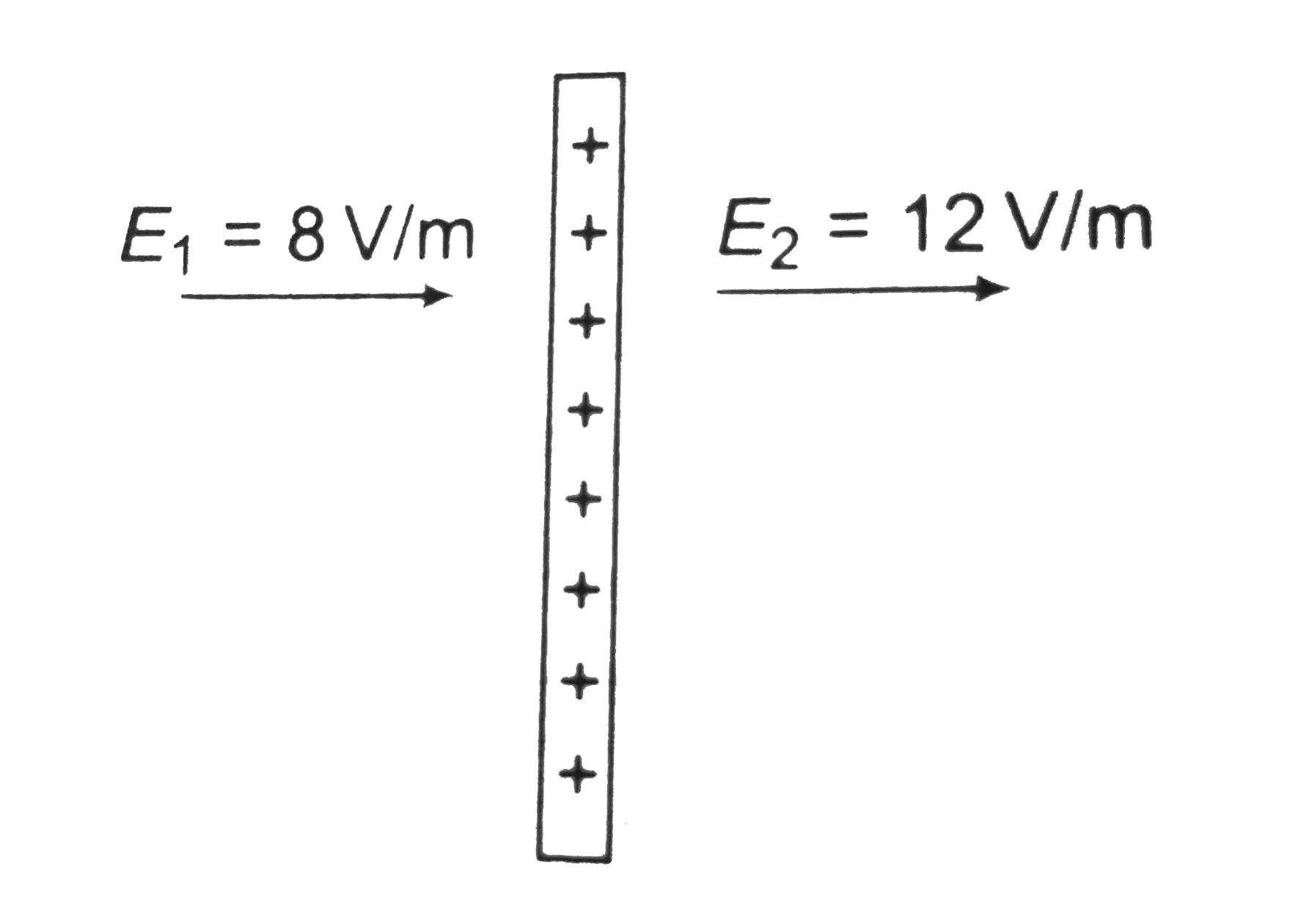
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionThe electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View SolutionIf q is the charge per unit area on the surface of a conductor, then the electric field intensity at a point on the surface is
View Solution

