A point charge (q) is kept above the centre of 8 cm x 8 cm square metal plate at a height of 4 cm. What will be the flux associated with this surface?
To solve the problem of finding the electric flux associated with the surface of an 8 cm x 8 cm square metal plate with a point charge q placed above its center at a height of 4 cm, we can follow these steps:
Step 1: Understand the Concept of Electric Flux
Electric flux (Φ) through a surface is given by the equation:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Step 2: Identify the Charge Enclosed
Since the point charge q is located above the center of the square plate and not inside it, we need to consider how to apply Gauss's law. The square plate itself does not enclose any charge.
Step 3: Construct a Gaussian Surface
To apply Gauss's law, we can imagine extending the square plate into a closed surface. If we consider a closed surface that includes the square plate and extends above it, we can think of it as a box with the square plate as one of its faces.
Step 4: Calculate Total Flux Through the Closed Surface
For a closed surface that encloses the charge q, the total electric flux through the entire closed surface is given by:
Φtotal=qϵ0
Step 5: Distribute the Flux Among the Surfaces
Since the closed surface consists of multiple faces (including the square plate), the flux will be distributed among these faces. If we assume symmetry, the flux through the square plate will be one-sixth of the total flux through the closed surface.
Step 6: Calculate the Flux Through the Square Plate
Thus, the flux through the square plate can be calculated as:
Φplate=16⋅Φtotal=16⋅qϵ0=q6ϵ0
Final Answer
The electric flux associated with the surface of the square metal plate is:
Φ=q6ϵ0
---
Electric flux (Φ) through a surface is given by the equation:
Φ=Qencϵ0
where Qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Since the point charge q is located above the center of the square plate and not inside it, we need to consider how to apply Gauss's law. The square plate itself does not enclose any charge.
To apply Gauss's law, we can imagine extending the square plate into a closed surface. If we consider a closed surface that includes the square plate and extends above it, we can think of it as a box with the square plate as one of its faces.
For a closed surface that encloses the charge q, the total electric flux through the entire closed surface is given by:
Φtotal=qϵ0
Since the closed surface consists of multiple faces (including the square plate), the flux will be distributed among these faces. If we assume symmetry, the flux through the square plate will be one-sixth of the total flux through the closed surface.
Thus, the flux through the square plate can be calculated as:
Φplate=16⋅Φtotal=16⋅qϵ0=q6ϵ0
The electric flux associated with the surface of the square metal plate is:
Φ=q6ϵ0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Tough & Tricky Problems
Explore 20 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Ncert File (Textbook Exercise)
Explore 34 Videos
- ELECTRIC CHARGES AND FIELDS Book:MODERN PUBLICATIONChapter:ELECTRIC CHARGES AND FIELDS Exercise:Practice Problems
Explore 88 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:MODERN PUBLICATIONChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:CHAPTER PRACTICE TEST
Explore 15 Videos
- ELECTROMAGNETIC INDUCTIONBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 14 Videos
Similar Questions
A point charge is placed at the centre of one of the Six Surfaces of a cube. What flux will be associated with the cube?

View SolutionA point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm. The magnitude of the flux through the square is
View Solution
Knowledge Check
A point charge Q is kept at the centre of a square face of edge length a. The amount of electric flux associated with the square face in
AQ6ε0BQ24ε0CQ8ε0D0A point charge of 1.77 μC is at the centre of a cubical gaussian surface having each side 50 cm. what is the net electric flux through the surface?
A105Nm2C−1B1.5×105Nm2C−1C2×105Nm2C−1D2.5×105Nm2C−1A point charge q is placed at a distance a/2 directly above the center of a square of side a. The electric flux through the square is
Aqε0Bqπε0Cq4ε0Dq6ε0
A point charge +10μC is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
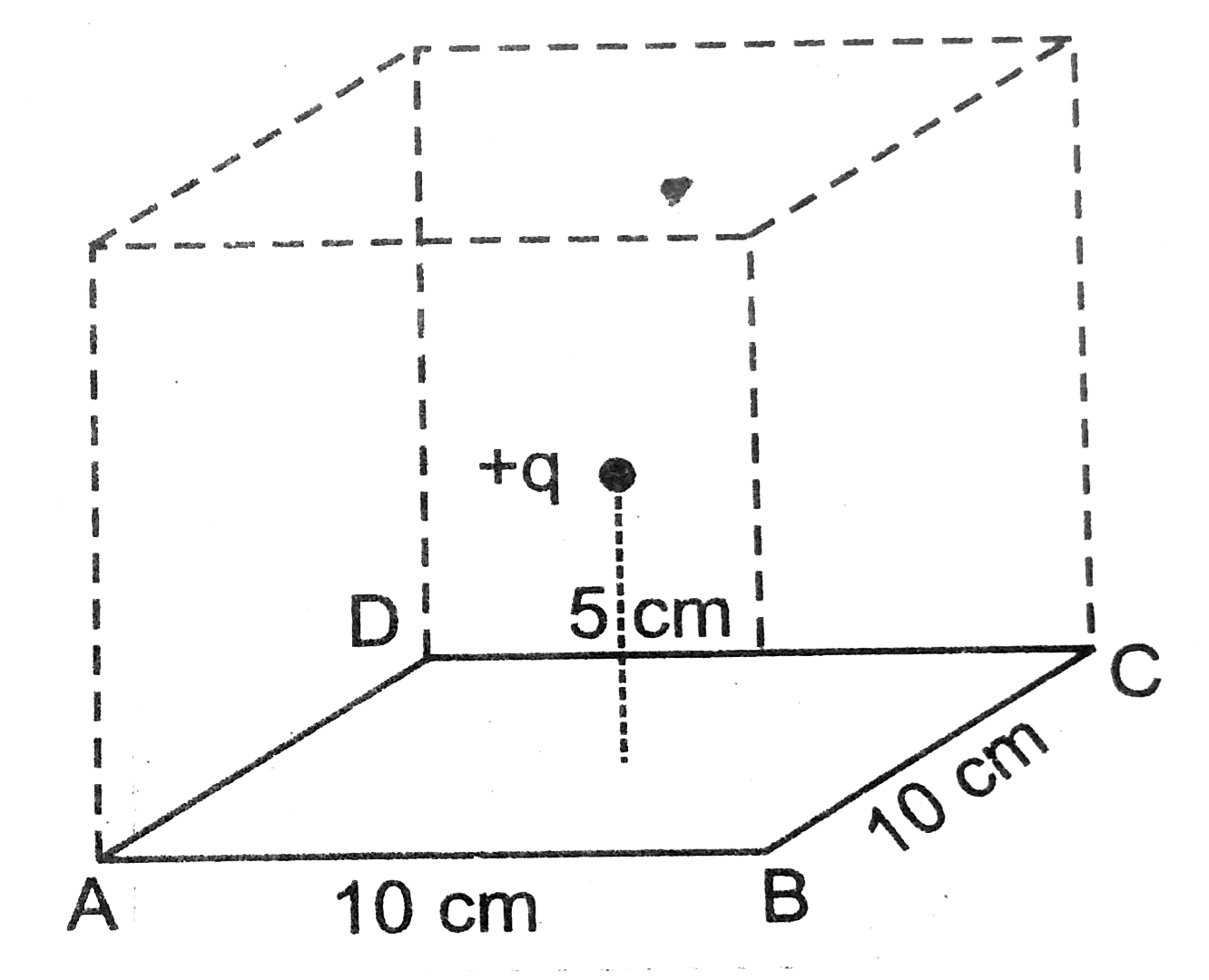
View Solution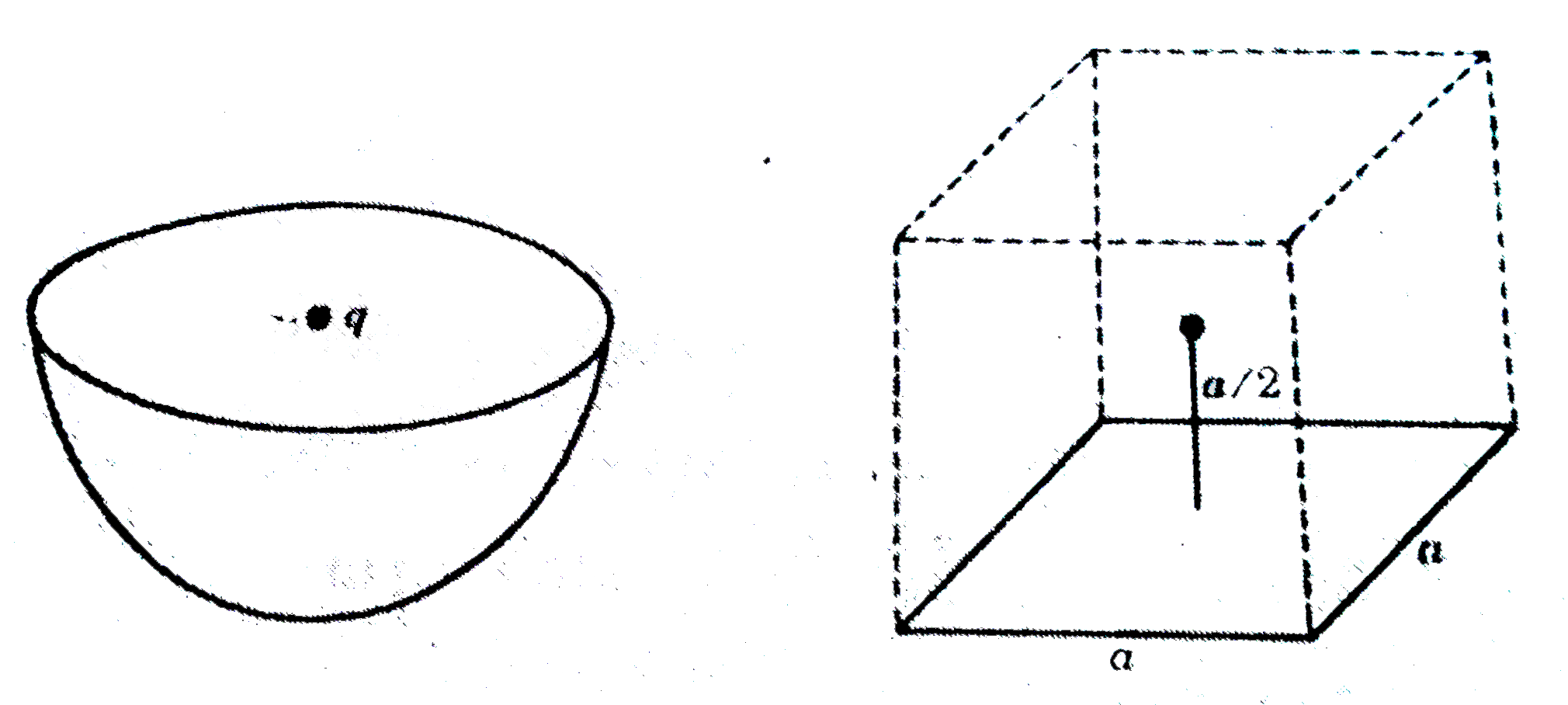
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
View SolutionAssertion (A) A charge q is placed on a height h/4 above the centre of a square of side b . The fluk associated with the square is independent of side length.
Reason (R ) Gauss 's law is independent of size of the Gaussian surface.
View SolutionAssertion (A) A charge q is placed on a height h/4 above the centre of a square of side b . The fluk associated with the square is independent of side length.
Reason (R ) Gauss 's law is independent of size of the Gaussian surface.
View SolutionA point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
View Solution

