A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is


A segment of charge is selected on ring at an angle θ and subtending angle dθ at its centre . Electric field due to this segment is shown as dE and is given by :
dE=14πε0QπdθR2
Here we have used the formula of electric field intensity due to a point charge for segment . On rearranging we get the following :
dE=14πε0QdθR2
Consider the corresponding segment on other half of ring as shown in the figure. It can be understood that components of electric field due to the charge segments along axis YY. are added but the components alon the axis XX. are cancelled by each other . Direction of net field is along the line of symmetry as shown in the figure.
E=∫Half-ring14π2ε0QdθR2cosθ
⇒E=Q4π2ε0R2∫π/2−π/2cosθdθ
E=∫Half-ringdEcosθ
Here , the limits of integration are selected to cover the complete semicircular ring. We can also change limits from 0 to π/2, but after multiplying the expression by 2.
⇒E=2Q4π2ε0R2∫π/20cosθdθ
⇒E=2Q4π2ε0R2[sinθ]π/20
⇒E=Q2π2ε0R2[sinπ/2−sin0]
⇒E=Q2π2ε0R2
The direction of net electric field intensity is marked in the given figure.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
A ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View SolutionA non-conducting ring of radius r has charge q distributed unevenly over it. What will be the equivalent current if it rotates with an angular velocity Ω?
View Solution
Knowledge Check
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it as shown in the figure. The net field →E at the center O is
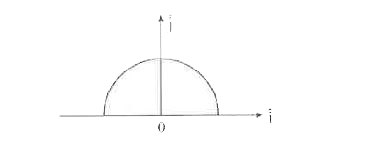 Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj
Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆjA ring of radius a contains a charge q distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance x from the centre.
Akq2x(a2+x2)32B2kq2x(a2+x2)32Ckq2x(a2+x2)32Dkq22x(a2+x2)32A small element l cut from a circular ring of radius a and λ charge per unit length. The net electric field at the centre of ring is
AzeroBλl4πε0a2C∞Dλ4πεl
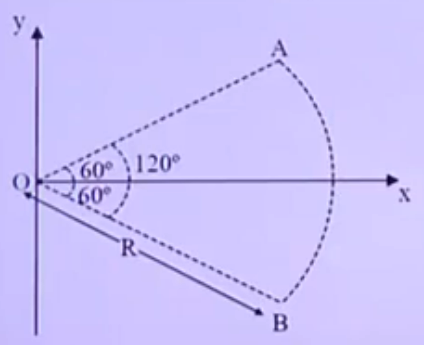
Figure shows a rod AB, which is bent in a 120∘ circular arc of radius R. A charge (-Q) is uniformly distributed over rod AB. What is the electric field →E at the centre of curvature O ?
View SolutionA thin wire carries a uniformly distributed charge Q = 3. 14nC along its length. The wire is bent in the form of a semi-circular arc of radius R = 1 m (without disturbing the charge distribution). Find the electric field at the center of curvature of the arc (in N/C).
View SolutionA thin circular wire of radius r has a charge Q. If a point charge q is placed at the centre of the ring, then find the increase in tension in the wire.
View SolutionA thin wire ring of radius r has an electric charge q. What is the tension of the wire if a point charge q0 is placed at the ring's centre?
View SolutionAs shown in the figure an electric dipole lies at a distance x from the centrr of a chargerd ring of radius R with charge Q uniformly distributed over it .The net force acting on the dipole is

View Solution
